- #1
Rugile
- 79
- 1
Homework Statement
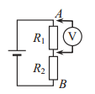
Two resistors are connected in series to an ideal battery. When the voltmeter is connected in parallel to one of the resistors, it showed 6V; when connected in parallel to another resistor it showed 4V. When the voltmeter was connected in parallel to both resistors (connected to pins A and B, see attachment) it showed 12V. What were the voltages across both resistors before the voltmeter was connected?
Homework Equations
Ohm's law
The Attempt at a Solution
I guess we can say from the third measurement that the voltage of the supply is 12V. Now the voltage across the first resistor is normally [itex] V_1 = V * \frac{R_1}{R_1 + R_2}[/itex], where V is the supply voltage. Although when the voltmeter is connected due to its internal resistance the voltage across 1st resistor changes; then the voltage across the voltmeter and the first resistor is [itex] V_1' = V * \frac{R_{01}}{R_{01}+R2}[/itex], and [itex] R_{01} = \frac{R_1 * r}{R_1 + r} [/itex], r is the voltmeter resistance. Thus [itex] V_1' = V * \frac{R_1r}{R_1r + R_2R_1 + R_2r}[/itex]. Same calculations can be made for the second resistor. Is that right? I can't figure out what to do next - any help appreciated.