- #1
rtareen
- 162
- 32
- Homework Statement
- For the systems in equilibrium in the figure below, find the unknown tensions and masses
- Relevant Equations
- ΣF = ma = 0
Here are two questions for my online homework. In part (a) we have to find T₁, T₂, and m.
For part a, I drew a free body diagram and used that ΣFₓ = -30N +T₁cos(60) = 0 To find T₁ = 60N. The software accepted my answer. Now we have to find T₂ and m. We have ΣFᵧ = T₂ + T₁sin(60) + mg = 0. We do not know T₂ and we do not know m. So how can we solve for both?
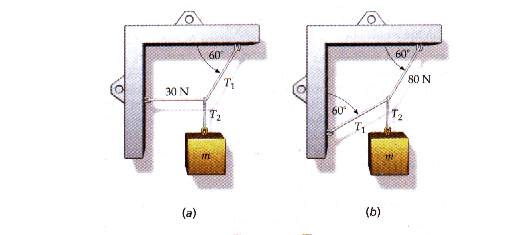
For part a, I drew a free body diagram and used that ΣFₓ = -30N +T₁cos(60) = 0 To find T₁ = 60N. The software accepted my answer. Now we have to find T₂ and m. We have ΣFᵧ = T₂ + T₁sin(60) + mg = 0. We do not know T₂ and we do not know m. So how can we solve for both?