- #1
Eats Dirt
- 92
- 0
Homework Statement
I have an integral in the form of
[/B]
[tex]
\int_{0}^{\infty} e^{-(\frac{x-c}{b})^2}dx
[/tex]
and I can't seem to figure it out.
I feel like I need a special function (gamma?)
Last edited:
Eats Dirt said:Ooops I think I realized I need to do a change of variables...
Eats Dirt said:[tex]
\int_{-c/b}^{\infty}e^{-ay^2}dy =! \frac{1}{2}\sqrt{\frac{pi}{a}}
[/tex]
Now the Gaussian doesn't work in that form so I think I need the indefinite form
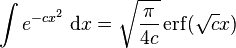
and I just evaluate this in my new limits?
Ray Vickson said:You tell us.
Eats Dirt said:Ok, now we use the error function,
[tex]
erf(y)=\frac{2}{\sqrt{\pi}}\int_{0}^{y} e^-t^2 dt
[/tex]
After I evaluate the error function I should put in the proper integration limits (from the original function) of y? But doesn't this just lead us in circles now? to evaluate this function I need another Gaussian function in a form that does not run from 0 to infinity.
pasmith said:The LaTeX for infinity is \infty, which produces [itex]\infty[/itex].
To your problem: the square of that integral is [tex]\int_0^\infty \int_0^\infty e^{-(\frac{x-c}b)^2 - (\frac{y-c}b)^2}\,dx\,dy[/tex] and the substitution [tex]
x - c = r \cos \theta \\
y - c = r \sin \theta[/tex] is called for.
An integral is a mathematical concept that calculates the total area under a curve using calculus. It is used to find the exact value of a function at a particular point or to find the area between a function and the x-axis.
Integrals can be challenging to solve because they require a deep understanding of calculus principles and techniques. They often involve complex mathematical operations, and a small mistake can lead to an incorrect result. It is essential to have a strong foundation in calculus and to practice regularly to become proficient in solving integrals.
Some common techniques for solving integrals include substitution, integration by parts, and partial fractions. Each technique has its advantages and is useful for solving different types of integrals. It is essential to understand these techniques and when to use them to solve integrals effectively.
Yes, there are several tools and software programs available that can help you solve integrals. These include graphing calculators, online integral calculators, and computer algebra systems. However, it is essential to understand the concepts behind the integral and not rely solely on technology to solve it.
Yes, some tips can help you improve your ability to solve integrals. These include practicing regularly, understanding the fundamental concepts and techniques, breaking the integral into smaller, manageable parts, and checking your work for errors. Seeking help from a tutor or teacher can also be beneficial in improving your integral-solving skills.