Solving a Uniform Beam Supporting Problem

[HoneyPi]

Homework Statement

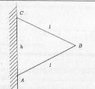
A uniform beam AB, of lenth l and mass m, is free in turn in a vertical plane about a smooth hinge at A. It is supported in a static position by a light string, of the same length l, attached to the end of end B of the beam and to an anchoring point C at a height h vertically above A.

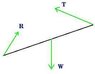
• Draw a diagram showing clearly all the external forces acting on the beam.
• By considering the equilibrium conditions for the beam, find an expression for the tension in the string in terms of m, l, h and g, the magnitude of the acceleration due to gravity.

Homework Equations

$$\textbf{R} = R_j \textbf{j} + R_k \textbf{k}$$

$$\textbf{W} = -mg \textbf{k}$$

$$\textbf{T} = - \textsl{T} \cos\theta \textbf{j} + \textsl{T} \sin\theta \textbf{k}$$

$$\textbf{r}_R = \textbf{0}$$

$$\textbf{r}_W = \frac{1}{2} l \cos(\frac{1}{2} \theta) \textbf{j}$$

$$\textbf{r}_T = l \cos(\frac{1}{2} \theta) \textbf{j}$$

The Attempt at a Solution

(i)

(ii) Determining the torques:

$$\boldsymbol{\Gamma}_R = \textbf{0}$$

$$\boldsymbol{\Gamma}_W = \frac{1}{2} l \cos(\frac{1}{2} \theta) \textbf{j} \times -mg \textbf{k} = - \frac{1}{2} l m g \cos(\frac{1}{2} \theta) \textbf{i}$$

$$\boldsymbol{\Gamma}_T = l \cos(\frac{1}{2} \theta) \textbf{j} \times \textsl{T} \sin\theta \textbf{k} = l \textsl{T} \cos(\frac{1}{2} \theta) \sin\theta \textbf{i}$$

Then since we consider the equilibrium conditions, we have

$$\boldsymbol{\Gamma}_T + \boldsymbol{\Gamma}_W + \boldsymbol{\Gamma}_R = \textbf{0}$$

Solving this in i-direction gives:
$$l \textsl{T} \cos(\frac{1}{2} \theta) \sin\theta = \frac{1}{2} l m g \cos(\frac{1}{2} \theta) \Rightarrow \textsl{T} \sin\theta = \frac{1}{2} m g$$

And now I am not sure about the following:

Since
$$\sin(\frac{1}{2} \theta) = \frac{\frac{1}{2} h }{l}$$
it follows that
$$2 \sin(\frac{1}{2} \theta) = \sin\theta = \frac{h}{l}$$

And so
$$\textsl{T} \frac{h}{l} = \frac{1}{2} m g \qquad \Rightarrow \quad \textsl{T} = \frac{mgl}{2h}$$

I'd appreciate it if someone could help me out with the last part of (ii) and also checking whether I did the other parts correctly.

Thanks a lot :)

Honey $$\pi$$

 

[rl.bhat]

Hi Honey π, welcome to PF.
In the last part 2sin(θ/2) is not equal to sinθ.
You know that sin(θ/2) = (h/2l).
Using trig. can you find cos(θ/2)
Then sinθ = 2sin(θ/2)cos(θ/2)

 

[HoneyPi]

Using trig. can you find cos(θ/2)

Let a be the altitude, then $$\cos(\frac{\theta}{2}) = \frac{a}{l}$$, but how can I eliminate the variable "a"?

I forgot to metion that I have the answer but no approach. The tutor's solution say that the answer is $$T=\frac{mgl}{2h}$$.

Thanks

Honey $$\pi$$

 

[rl.bhat]

Consider the angle between rod and string as θ1 and the angle between rod and the vertical as θ2.
Take the component of mg along the rod and perpendicular to the rod.
Take the components of T along the rod and perpendicular to the rod.
Perpendicular components constitute torque.
In triangle ABC, according to the properties of triangle,
h/sinθ1 = l/sinθ2. Noe try to solve the problem.