- #1
tjhollis1
- 7
- 1
- TL;DR Summary
- I am developing a model for transmission line cables and I need help calculating the cable sag as a function of a couple of variables. It seems like I have enough information to solve this problem, however I am unable to find a solution to this. Please advise.
Hi all,
I am no structural engineer and I have toiled extensively over this for far too long and at this point I am wondering if this problem has a solution with the given variables...
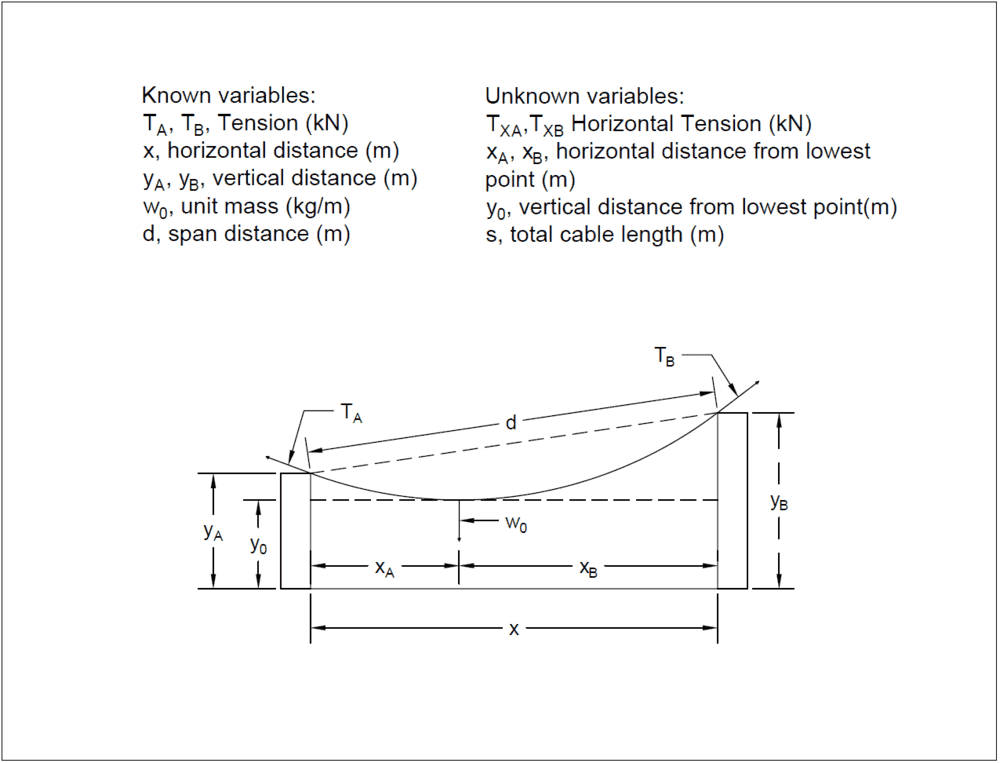
It is my understanding that the standard equation for a Catenary is: ##y = a \cdot cosh(\frac {x}{a})##. However, I feel this equation does not apply to my problem (attached pdf or figure to the right).
It seems that everywhere I look, there are Catenary problems such as this source which gives the span as well as the sag and then the problem is solved using the given variables. In my problem, I only have the span, total Tension and differential height.
The following equations are what I have tried (variables are form the source):
$$
\begin{align}
s & = c \cdot sinh(\frac {x} {c}) \\
y^2 - s^2 & = c^2 \\
W & = w_0 \cdot s \\
y & =c \cdot cosh(\frac {x} {c}) \\
T_x & =w_0 \cdot c \\
T & = w_0 \cdot y \\
\end{align}
$$
You see, my problem formulation comes from two transmission towers spaced apart at different elevations, ##P(x_a, y_a)## and ##P(x_b, y_b)##. This is throwing me off, because ultimately I figure it should be the normal equation since I have the span distance, ##d## and then simply add the formula to a line of slope ##mx+y_0##.
There are a couple of cases that I want to look into:
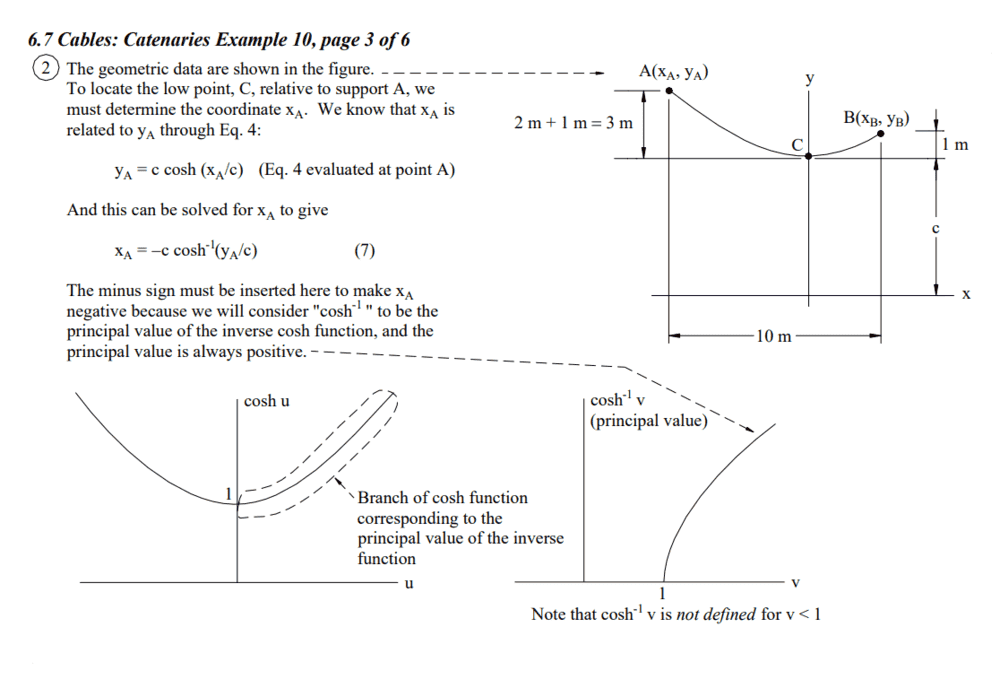
The closest I feel I have come in this is the following (with my problem's variables substituted):$$ x_B = y_0 \cdot cosh^-{1}(\frac {y_B} {y_0})$$
$$ x_A = y_0 \cdot cosh^{-1}(\frac {y_A} {y_0})$$
$$ x = x_B - x_A$$
$$ y_0 \cdot cosh^{-1}(\frac {y_B} {y_0}) + y_0 \cdot cosh^{-1}(\frac {y_A} {y_0}) - x = 0$$
This equation does not take into account the Tension, someone please advise on what to do. From what I can understand, I should be able to derive and equation which I could take the limit of the T as it approached infinity, the sag should be zero.
$$\lim_{T \rightarrow +\infty} {y_0(T) = 0}$$
and another equation
$$\lim_{T \rightarrow 0} {y_0(T) = \infty}$$
Please help,
Tanner H.
I am no structural engineer and I have toiled extensively over this for far too long and at this point I am wondering if this problem has a solution with the given variables...
It is my understanding that the standard equation for a Catenary is: ##y = a \cdot cosh(\frac {x}{a})##. However, I feel this equation does not apply to my problem (attached pdf or figure to the right).
It seems that everywhere I look, there are Catenary problems such as this source which gives the span as well as the sag and then the problem is solved using the given variables. In my problem, I only have the span, total Tension and differential height.
The following equations are what I have tried (variables are form the source):
$$
\begin{align}
s & = c \cdot sinh(\frac {x} {c}) \\
y^2 - s^2 & = c^2 \\
W & = w_0 \cdot s \\
y & =c \cdot cosh(\frac {x} {c}) \\
T_x & =w_0 \cdot c \\
T & = w_0 \cdot y \\
\end{align}
$$
You see, my problem formulation comes from two transmission towers spaced apart at different elevations, ##P(x_a, y_a)## and ##P(x_b, y_b)##. This is throwing me off, because ultimately I figure it should be the normal equation since I have the span distance, ##d## and then simply add the formula to a line of slope ##mx+y_0##.
There are a couple of cases that I want to look into:
- ##T_A = T_B##, and create a solution based on this condition. Where ##y_A = y_B## as well as ## y_A \ne y_B##.
- Since the higher tower, ##B##, is going to have higher tension, set the known variable, ##T_B##, and solve for ##T_A## as well as a solution for sag and other parameters.
The closest I feel I have come in this is the following (with my problem's variables substituted):$$ x_B = y_0 \cdot cosh^-{1}(\frac {y_B} {y_0})$$
$$ x_A = y_0 \cdot cosh^{-1}(\frac {y_A} {y_0})$$
$$ x = x_B - x_A$$
$$ y_0 \cdot cosh^{-1}(\frac {y_B} {y_0}) + y_0 \cdot cosh^{-1}(\frac {y_A} {y_0}) - x = 0$$
This equation does not take into account the Tension, someone please advise on what to do. From what I can understand, I should be able to derive and equation which I could take the limit of the T as it approached infinity, the sag should be zero.
$$\lim_{T \rightarrow +\infty} {y_0(T) = 0}$$
and another equation
$$\lim_{T \rightarrow 0} {y_0(T) = \infty}$$
Please help,
Tanner H.
![\begin{displaymath} \left[\begin{array}{c}x_1 \vdots x_N\end{array}\right]_{... ... \vdots \vdots \vdots f_M({\bf x}_n) \end{array}\right] \end{displaymath} \begin{displaymath} \left[\begin{array}{c}x_1 \vdots x_N\end{array}\right]_{... ... \vdots \vdots \vdots f_M({\bf x}_n) \end{array}\right] \end{displaymath}](http://fourier.eng.hmc.edu/e176/lectures/NM/img1387.png)