Using Kirchhoff's Laws to find current in a circuit

[klandestine]

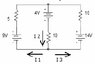
I have attached a picture of a circuit. I am trying to find the values of I₁, I₂, and I₃.

What I have come up with so far, using Kirchhoff's Voltage and Junction Laws is:

I₂=I₁+I₃

for the left loop:
9V - (5 ohms)I₁ -4V - (10 ohms)I₂ = 0
which simplifies to:
1V - (1 ohm)I₁ - (2 ohms)I₂ = 0

for the right loop:
14V - (10 ohms)I₃ -4V - (10 ohms)I₂ = 0
which simplifies to:
1V - (1 ohm)I₃ - (1 ohm)I₂ = 0

I am pretty certain that I have these correct, but I can't seem to solve my system of equations--whenever I try to add or subtract the equations, several terms cancel, leaving me with a current equaling zero.

I would really appreciate some help. Thank you. :!)

 

[Fermat]

You have three eqns and three unknowns.

The eqn you're not using is,

I2 = I1 + I3

substitute.

 

[klandestine]

I did have that equation. It is the first equation I listed on my first post. I tried to substitute using it, but too much keeps cancelling.

 

[Fermat]

These are your eqns, yes

I_2 = I_1 + I_3
\mbox{left loop: }\ I_1 + 2I_2 = 1
\mbox{right loop: }\ I_3 + I_2 = 1

They should simply work out. Since I₂ is common to both the 2nd and 3rd eqn, you should substitute for I₂ in these two eqns.
If you did that and it's still not coming out, could you show your working ?

 

[Elysium]

Are you using matrix notation for this problem?

 

[klandestine]

Substituting gives these two equations:

3I₁+2I₃=1

I₁+2I₃=1

The problem is when I try to subtract these equations I get:

2I₁=0

How can the current be zero?

 

[Fermat]

One way is to have two equal batteries hooked up such that their potentials are opposed to each other, then you will get zero current.

I got zero current as well for I₁

 

[klandestine]

Thank you Fermat.

I guess I was doing the problem right all along, I just didn't trust myself.

Thanks :!)

 

[Ouabache]

\mbox{left loop: }\ I_1 + 2I_2 = 1
\mbox{right loop: }\ I_3 + I_2 = 1

just curious, how did you determine these equations?

 

[Fermat]

Using Kirchoff's laws.

Here's a brief explanation of them.

If you look at Klandestine's 1st post, you wiil see that my eqns are just a simplification of his work.

 

[Ouabache]

Thanks, you're 3rd line explains what you did, reduced the first two equations by a common divisor. (I didn't notice Klandestine did that too). This reminds of some texts we had that said thus, we have these expressions! and assumed we knew their intermediate steps. Have you ever seen some of those?
Without your reduction, I used klandestine's original equations and arrived at the same solution. Oh, yeah, I am familiar with good ol' http://chem.ch.huji.ac.il/~eugeniik/history/kirchhoff.htm ..

 

[Fermat]

... It reminds of some texts we had that said thus, we have these expressions! and assumed we knew their intermediate steps. Have you ever seen some of those? ...

Only too well.
The phrase that's currently in vogue over here is "... it can be shown that ..."
I'll be taking a new maths course soon, and I've been following the online forum for current students of this course. One of their big complaints is how often that phrase occurs. And another is how they are asked questions which relate to material that they have never covered.