- #1
Emily Smith
- 1
- 0
<Moderator's note: Moved from a technical forum and thus no template.>
Problem:
One dimensional quartic oscillator, V(x) = cx^4 (c is a constant)
Use the trial function e^(-aplha(x^2)/2) to determine the value of the appropriate variational integral W.
I've attached a picture of my work.
I feel that my answer is not correct, because I ended up using identities (listed below) at the end because I was grasping for straws. So my question is: did I mess up by using the identities?
Identity 1 = x^n e^bx^2 = (2n!)/(2^(2n+1)n!)(pi/(b^2n+1))^1/2
Identity 2 = e^-bx^2 = 1/2 (pi/b)^1/2
I used the phi* V phi / phi*phi equation. Started with phi *(V)phi, e^(-aplha(x^2)/2)(Cx^4)e^(-aplha(x^2)/2) dx
I pulled the C out since it was constant and simplified to e^(-aplha(x^2))(x^4)
From there I used the Identity 1 and got 0.0625C (pi/(aplha^5))^(1/2).
For phi*phi I used Identity 2 and got sqrt(pi/alpha)/2
Finally I divided hi* V phi by phi*phi which gave me 0.125C(sqrt(pi/(alpha^5))/ sqrt(pi/alpha)
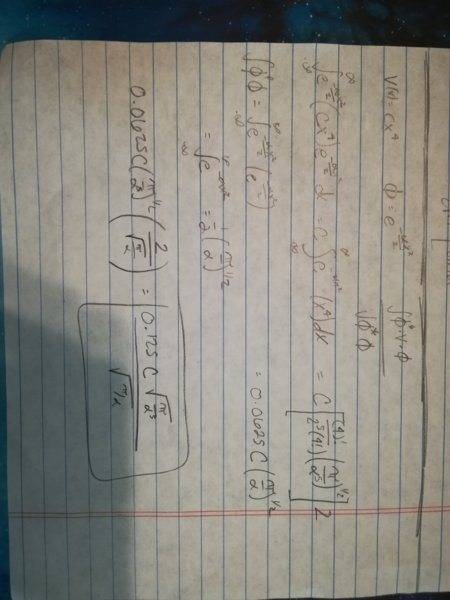
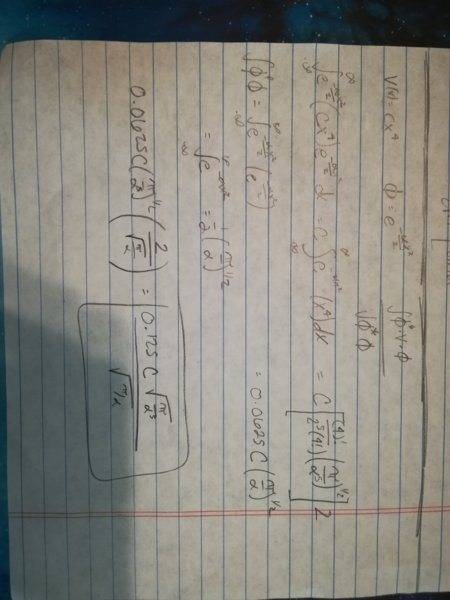
Problem:
One dimensional quartic oscillator, V(x) = cx^4 (c is a constant)
Use the trial function e^(-aplha(x^2)/2) to determine the value of the appropriate variational integral W.
I've attached a picture of my work.
I feel that my answer is not correct, because I ended up using identities (listed below) at the end because I was grasping for straws. So my question is: did I mess up by using the identities?
Identity 1 = x^n e^bx^2 = (2n!)/(2^(2n+1)n!)(pi/(b^2n+1))^1/2
Identity 2 = e^-bx^2 = 1/2 (pi/b)^1/2
I used the phi* V phi / phi*phi equation. Started with phi *(V)phi, e^(-aplha(x^2)/2)(Cx^4)e^(-aplha(x^2)/2) dx
I pulled the C out since it was constant and simplified to e^(-aplha(x^2))(x^4)
From there I used the Identity 1 and got 0.0625C (pi/(aplha^5))^(1/2).
For phi*phi I used Identity 2 and got sqrt(pi/alpha)/2
Finally I divided hi* V phi by phi*phi which gave me 0.125C(sqrt(pi/(alpha^5))/ sqrt(pi/alpha)
Attachments
Last edited by a moderator:
