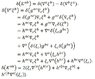- #1
feiye
- 4
- 0
if we know
K^{a b}= (∇^a*ζ^b -∇^b*ζ^a)/2,
ζ is a killing vector,
under the variation of metric g_{a b}→g_{a b}+δ(g_{a b}) which preserves the Killing vector δ(ζ^a)=0,
h_{a b} = δ(g_{a b}) = ∇^a*ζ^b +∇^b*ζ^a,
how to prove
δ(K^{a b})= ζ_c*∇^a*h^{b c} - h^{c a}*∇_c*ζ^b - ( ζ_c*∇^b*h^{a c} - h^{c b}*∇_c*ζ^a )
thanks!
K^{a b}= (∇^a*ζ^b -∇^b*ζ^a)/2,
ζ is a killing vector,
under the variation of metric g_{a b}→g_{a b}+δ(g_{a b}) which preserves the Killing vector δ(ζ^a)=0,
h_{a b} = δ(g_{a b}) = ∇^a*ζ^b +∇^b*ζ^a,
how to prove
δ(K^{a b})= ζ_c*∇^a*h^{b c} - h^{c a}*∇_c*ζ^b - ( ζ_c*∇^b*h^{a c} - h^{c b}*∇_c*ζ^a )
thanks!