How do you calculate vector subtraction in physics?

[Byrgg]

I'm in gr. 12 physics right now(just started school today), and we started some review work. This is a new school, so I'm guessing some of the things taught by the different teahers vary, which explains why I don't understand this question. Here's the question word for word, there's also a small amount of information before the question, which I'll also post:

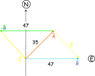
The vector subtraction A - Bis defined as the vector addition of A and -B, where -B has the same magnitude as B, but is in the opposite direction. Thus A- B = A + (-B).

Ex 4. Given that A = 35m/s [27 degrees N of E] and B = 47 m/s [E], determine the change in velocity C = A - B.


Now, I'm only a high school physics student, but the way I know to calculate a change in velocity is v_2 - V_1. This question threw me off completely, and I have no idea what I should do. The only thing I came up with, was this, and I'm sure it's wrong, but I'll post it anyway:

C = A - B
= 35 - 47
= -12

Therefore the change in velocity is -12 m/s.

I don't think this can be right. Number one, the velocity is increasing from A to B, so I don't think the answer should be negative. And number two, this says nothing about the change in direction, only speed.

Someone please help soon, thanks in advance.

 

[Chi Meson]

You have not taken direction into account.

A is 35 m/s, 27 degrees n of e.
Find the componant north and the componant east.

 

[Byrgg]

Ok, so I should find the North and East components of the vector, and then use that in the equation instead?

 

[Hootenanny]

Ok, so I should find the North and East components of the vector, and then use that in the equation instead?

Yes, sounds good to me. Decompose both vectors into their North and East components find the change in each case, then recombine the two components to find the resultant vector. Don't forget to find and quote the bearing.

 

[Byrgg]

Don't forget to find and quote the bearing.

What does that mean?

Also, after I decompose the vector into it's components, and add them, what do I do? To find the new resultant vector, do I use the new East component, along with the previous North component to find the resultant vector?

 

[Hootenanny]

What does that mean?

Once you have performed the vector subtraction you will be left with a vector that has two components, North/South and East/West. Now, to fully answer the question, you must find the resultant vector. Now, you can find the magnitude using pythag; then you must use trig to find the angle or direction of this vector. Do you follow? I am assuming that you have done this before.

Also, if I decompose the the vectors into their North and East components, then I can add the east components, but what does that say for the earlier mentioned North component? Is it really alright to only add one component? Part of it is getting left out.

Yes, this is totally acceptable because you will also be adding the north components together, you aren't leaving any out. For example, if I has to vectors and their components were (N= North and E = East);

$$\vec{A} = 5N + 10E$$

$$\vec{B} = 4N - 6E$$

Then, the vector $\vec{AB}$ (or C = A + B) would be;

$$\vec{AB} = (5+4)N + (10-6)E$$

$$\vec{AB} = 9N + 4E$$

Do you follow?

 

[Byrgg]

I think I understand, now. I also editted my earlier post, because I started to understand what you were saying, a little better.

So basically I add the North/South components, and the East/West components, and that gets me the resultant vector?

 

[Hootenanny]

So basically I add the North/South components, and the East/West components, and that gets me the resultant vector?

Yes, but then you need to combine the two components into a single vector, you can do this using pythag. Once, you have done this you need to find the angle and quote a bearing (e.g. 32^o anti-clockwise from north or whatever it may be).

 

[Byrgg]

Oh, alright. It seems a bit easier than I thought. It was just a familiar question masked in unfamiliar terms, it seems. I'll post my work when I'm done, so could someone make sure I did it right?

 

[Hootenanny]

Oh, alright. It seems a bit easier than I thought. It was just a familiar question masked in unfamiliar terms, it seems. I'll post my work when I'm done, so could someone make sure I did it right?

I find that I'm always a bit rusty after the breaks, but it soon comes flooding back

 

[Byrgg]

Ok, I think I got the right answer, it's just the resultant vector of the two, right? But I was wondering something, what exactly is the resultant vector? What is the importance of this value? I know that in the case of displacement, the resultant vector shows the overall distance travelled, and in which direction, but this isn't displacement, this question is about velocity. What exactly does the resultant vector represent? The final velocity is still 47 m/s [E], isn't it?

Also, I was wondering, what does this problem have to do with vector subtraction? From what I gathered, vector components were being added, but the explanation before the problem made things seem a little confusing,

 

[Byrgg]

Someone please help.

 

[hakojackie]

Vector subtraction is kind of a fancy way of saying that you can add two vector distances even if they are going opposite directions. The subtraction part just means that they want you to look at which direction the vectors are going. The resultant vector is the addition of the the two components. I think the resultant vector in this case is just used to help you find the average velocity. Hopefully this helps I am new to physics too so I may not 100 percent correct.

 

[Byrgg]

Hmm, you make a good point, thanks for your help. I guess the resultant vector is just the average velocity, I think that works, at least in a simple case. Can anyone else clarify?

 

[andrevdh]

Initially the object moved in the direction of vector A. Now it is moving in the direction of vector B. The change in it's velocity is given by vector C, that is vector C is the difference between the two velocity vectors or it is the sum of vector A and -B. Vector C therefore tells us by how much and in which direction the object's velocity had to be changed in order to move with the new speed in the direction of vector B.

 

[Byrgg]

I'm guessing that the attachment in andrevdh's post is a diagram of some sort. I appreciate the help, but, while I'm waiting, is there anything else anyone could say or show to help clarify this? andrevdh said that C represented the change between A and B, but I still don't understand some things. Why does the formula use A and -B? Why do you make B negative? And how exactly does the resultant vector represent the change in velocity? Sorry if this is really simple, but it's a new school, and some of these terms/concepts I never learned before, so I'm a bit confused.

 

[andrevdh]

With ordinary quantities it works the same way:

If you had one hundred dollars (A) and you now have 40 (B) then the original amount was changed by 100 - 40 = 60 (C). That is the difference between the "old amount" and the "new amount" gives the change in the quantity. This relationship that the original amount is conserved is not necessary applicable in the case of vectors. A force applied to the object can alter it's velocity in both magnitude and direction, resulting in a larger or smaller velocity than originally.

 

[Byrgg]

Ok, but I have another question, sorry if it was already answered indirectly or something, but it's kind of confusing to me. Say an object travels 5 m/s [N], and then 5 m/s , would you say it has no velocity, in this case? I just find it confusing, because in reality, the object is still moveing 5 m.s , but for some reason, I don't think this is the case here.

 

[Hootenanny]

Ok, but I have another question, sorry if it was already answered indirectly or something, but it's kind of confusing to me. Say an object travels 5 m/s [N], and then 5 m/s , would you say it has no velocity, in this case? I just find it confusing, because in reality, the object is still moveing 5 m.s , but for some reason, I don't think this is the case here.

No, intially it would have a velocity of 5 m.s^-1 N. Then after an acceleration it would have a final velocity of 5 m.s^-1 S. At no point is the velocity zero.

 

[Byrgg]

No, intially it would have a velocity of 5 m.s^-1 N. Then after an acceleration it would have a final velocity of 5 m.s^-1 S. At no point is the velocity zero.

Why were there exponents with your velocities?

And what about when you add the vectors? You get a result of 0 m/s. What does this zero represent?

 

[Hootenanny]

Why were there exponents with your velocities?

It is just a different notation for the units (m/s = m.s^-1)

And what about when you add the vectors? You get a result of 0 m/s. What does this zero represent?

It has no meaning, since the velocities occur at different points in time.

 

[Byrgg]

It is just a different notation for the units (m/s = m.s^-1)

Oh, sorry, I just realized how obvious that was. Thanks for pointing that out.

It has no meaning, since the velocities occur at different points in time.

But what about when you calculate the resultant vector? It will be 0 m/s.

 

[Hootenanny]

But what about when you calculate the resultant vector? It will be 0 m/s.

It is an interesting question that you pose and one that I haven't thought much about. But I still say that at no point is the velocity actually zero. Perhaps someone else could chip in at this point.

 

[Byrgg]

It is an interesting question that you pose and one that I haven't thought much about. But I still say that at no point is the velocity actually zero. Perhaps someone else could chip in at this point.

I can see what you're saying, I wouldn't say the velocity is ever zero, either, so this why I'm getting confused. I always thought that this zero had to mean something. In the case of displacement, if you travel 5 m [N], and then 5 m , the overall displacement is considered 0. I just don't see how this fits into velocity.

 

[Tomsk]

If you start at 5m/s [N], and accelerate to 5m/s , then you would have to go through v=0. Look at it like this, the original v is 5m/s [N], the final v is -5m/s [N]. So, the change in magnitude is 10m/s, and the resultant vector would be -10m/s [N] OR +10m/s , but stick to one direction! You changed the direction you're considering for the final v, saying it's 5m/s , which is misleading. I would use x and y coordinates for a question like this, with x and y always increasing in one direction.

 

[Byrgg]

If you start at 5m/s [N], and accelerate to 5m/s , then you would have to go through v=0. Look at it like this, the original v is 5m/s [N], the final v is -5m/s [N]. So, the change in magnitude is 10m/s, and the resultant vector would be -10m/s [N] OR +10m/s , but stick to one direction! You changed the direction you're considering for the final v, saying it's 5m/s , which is misleading. I would use x and y coordinates for a question like this, with x and y always increasing in one direction.

I was thinking about more about adding the vectors 5 m/s [N], and 5 m/s . You get a result of 0 m/s, don't you? But I don't understand this considering that the object still motion, isn't it?

 

[Tomsk]

It would definitely go through zero, think of throwing an object up in the air, it might leave your hand at 5m/s, then it will stop in the air momentarily, and come back down, reaching 5m/s when you catch it.

 

[Tomsk]

I was thinking about more about adding the vectors 5 m/s [N], and 5 m/s . You get a result of 0 m/s, don't you? But I don't understand this considering that the object still motion, isn't it?

The vector 5m/s is exactly the same as -5m/s [N]. For a question like this, always use the same direction, for example north, otherwise you'll get confused.

 

[Byrgg]

So, basically if it's 5 m/s [N], and then 5 m/s , then the object must slow down to change velocity? But isn't a single vector supposed to represent a constan velocity?

Also, why does using a negative North vector make it any more understandable? And what about when the vectors aren't only in one dimension, what about a two dimensional resultant vector?

 

[Tomsk]

The vector representing the change in velocity only represents the total change, if you knew the time it took to change from +5 to -5, you'd know the acceleration, which would be -10/t.

Using a negative north vector mean you can look at the initial and final speeds to work out the change, you know that to change from +5 to -5 requires a change of -10. When you are in more than one dimension, use conventions that always use the same direction in the same dimension, eg only N and E, i and j, x and y, or whatever.

A two dimensional resultant vector will also just show you the total change, it doesn't give you the speed at any time between the initial and final velocities.

 

[Byrgg]

Oh, wait a second, in the +5 case with zero being the final, -5 would be the change, right? And what do you mean by the total change in a two dimensional case? If you have some starting vector, and then some ending vector, is the resultant the change between those two? And in the one dimensional case(sorry for jumping around like this), I was thinking that, if you add +5 and -5, you get obviously get 0. What significance does this zero have, what is it, exactly? The final velocity?

If you have:

-->

and then you add:

<--

Then you get something like this:

-->
<--

When you add those two vectors, you get 0. I'm wondering what exactly this zero is. Sorry if this is unclear or anything. I'm sure you've already explained this in some earlier post, some way or another, but it just keeps on confusing me.

 

[Byrgg]

I"ll try to explain this a little better. Say you're traveling at 5 m/s [N], and then suddenly you start traveling at 5 m/s . Through vector analysis, wouldn't you have to change your velocity by 10 m/s , in order to achieve this? But on the other hand, can't you just turn around, and start moving in the opposite direction? How is this a change of 10 m/s ? Also, in order to achieve a velocity of 0 m/s, you would need to change your velocity by 5 m/s , right? Don't you just stop? How is stopping the same as changing your velocity 5 m/s ?

And, in my previous post, what exactly is 0? Is that the final velocity, whereas the negative vector, is just the change in velocity?

 

[Tomsk]

I think you're confusing two situations. The first one you gave was:

Initial velocity = +5m/s
Final velocity = -5m/s
Change in velocity = -10m/s

Remember,
Change = Final - Initial;
-10 = (-5) - (+5)

Then, just now you are adding +5 and -5 and getting zero, this is the situation:

Initial velocity = +5m/s
Final velocity = 0m/s
Change in velocity = -5m/s

Change = Final - Initial;
-5 = (0) - (+5)

You are not considering acceleration in either of these situations, sorry if I confused you about that.

 

[Byrgg]

So then, for what purpose are vectors ever added, if you subtract to determine change?

 

[Tomsk]

You could add them if you know the initial velocity and the velocity added, and you want the final velocity. It depends on what you want to find out and what you know.