Vectors & Angles Problem Analysis

[emaz]

Homework Statement

Determine the range of possible values of the angle θ between the directions of motion of the two resulting particles in the L system.

Relevant Equations

$$ \begin{align} \frac {\partial\cot{\theta}} {\partial\theta_{0}} = \frac {(-v_{10}+v_{20})V^2-V\cos\theta_{0}\left[V^2-v_{10}v_{20}\right] }{(v_{10}+v_{20})V^2\sin^2\theta_{0}} \nonumber\end{align}$$

Hello,

it is my first post here and I am not really sure whether this is the right section. I did not have the chance to take a look at the rules of the forum but I will as soon as I can (I feel a bit guilty for that, I'm sorry...). This is not "homework", I am just studying the amazing L&L books on theoretical physics.
I created this thread because I got stuck doing problem #3 from sub-section 16 of L&L book on mechanics. The very short preamble to understand the problem is that there is a particle with velocity $V$ which disintegrates into two particles. The problem goes like this: "Determine the range of possible values of the angle θ between the directions of motion of the two resulting particles in the L system". The graphical representation of the problem that I have constructed turned out to be the same as the one in the following link: https://www.physicsforums.com/threads/trigonometric-function-mechanics-landau.962697/.
In the link, the OP says he has solved the problem, but there seems to be no hint at how he did it (I asked him but I got no answer).
For the sake of this post being independent, I shall insert the figure here as well:

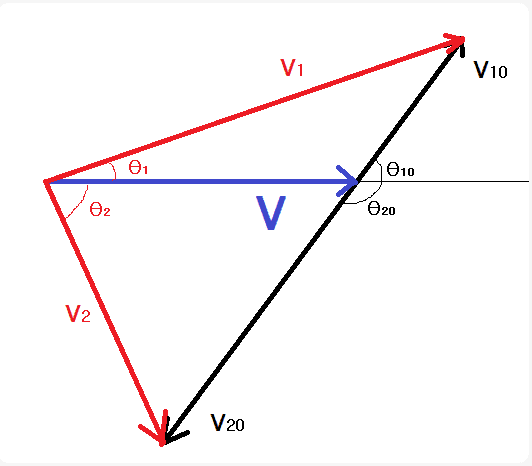
I have found similar threads in which the main suggestion to tackle the problem is to take the derivative of the tangent of θ with respect to the angle θ₀, where the expression of $\tan\theta$ is given by: $$ \begin{align}\tan{\theta} = \frac {(v_{10}+v_{20})V\sin{\theta_{0}}}{V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }} \nonumber\end{align}$$
To avoid as many ambiguities as possible, even though it should be clear from the figure: $v_{10}, v_{20}$ are the velocities of the two particles in the C-frame, $\theta= \theta_{1}+\theta_{2}, \theta_{0}=\theta_{10}=\pi-\theta_{20}$, and $v_{1},v_{2}$ are the velocities of the particles in the L-frame (without loss of generality, it is supposed that: $v_{10}<v_{20}$ ).
Instead of the tangent, I preferred to work with the cotangent of $\theta$, since it does not have discontinuities in the interval $\left] 0, \pi \right[$. I took the derivative and found the expression:
$$ \begin{align} \frac {\partial\cot{\theta}} {\partial\theta_{0}} = \frac {(-v_{10}+v_{20})V^2-V\cos\theta_{0}\left[V^2-v_{10}v_{20}\right] }{(v_{10}+v_{20})V^2\sin^2\theta_{0}} \nonumber\end{align}$$
By setting the result to 0 one gets: $$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
The solution given in L&L book is written in terms of $\sin{\theta_{0}}$ and its cosine does not correspond to the formula above, so this is the first thing that does not add up.
Anyway, by assuming the expressions so obtained are correct (as well as the figure associated to the statement of the problem), a careful analysis of the ranges of $\theta$ leads to:
$$ \begin{align} &\text{if}~~ v_{10}<V<v_{20} \rightarrow 0<\theta<\pi \nonumber \\
\nonumber \\
&\text{if}~~ V<v_{10} \rightarrow \pi-\alpha<\theta<\pi \nonumber \\
\nonumber \\
&\text{if}~~ V>v_{20} \rightarrow 0<\theta<\alpha \nonumber\end{align} $$
where $$\alpha=\cot^{-1}\left({2\sqrt{\frac{2v_{10}}{v_{10}+v_{20}}}}\right)$$

In the ranges above, the results are similar to those given by L&L, but the angle $\alpha$ is not the same. I wrote some Matlab code that seemingly supports the equations written above. For $V<v_{10}$, the value $\theta=\pi-\alpha$ is achieved when $$V=-\frac{v_{20}-v_{10}}{2\beta}+\frac{1}{2\beta}\sqrt{\left(v_{20}-v_{10}\right)^2+4v_{10}v_{20}\beta^2}$$ where $$\beta=\sqrt{\frac{v_{20}+v_{10}}{3v_{10}+v_{20}}}$$
For $V>v_{20}$, the value $\theta=\alpha$ is achieved when $$V=\frac{v_{20}-v_{10}}{2\beta}+\frac{1}{2\beta}\sqrt{\left(v_{20}-v_{10}\right)^2+4v_{10}v_{20}\beta^2}$$

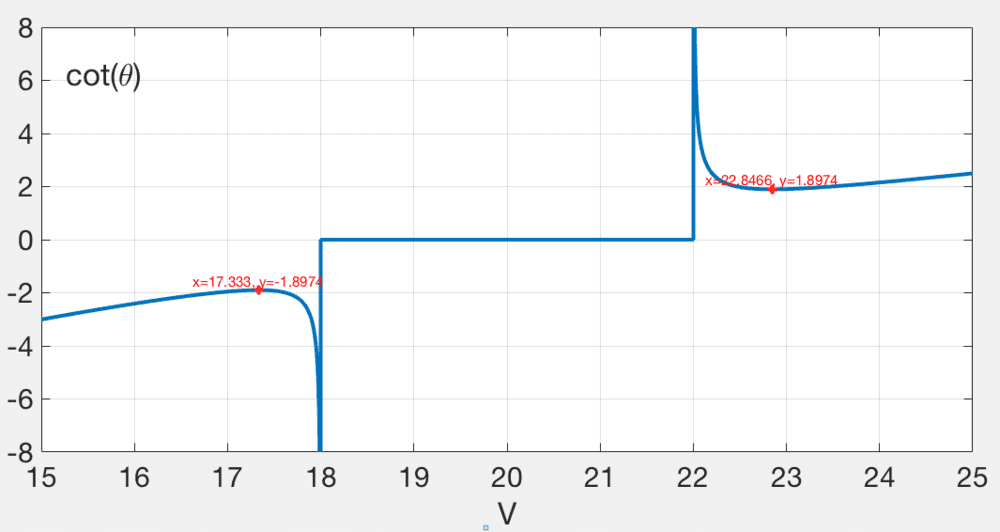
For instance, if we take $v_{10}=18, v_{20}=22$, the Matlab plot for $\cot\theta$ versus $V$ would result as in the figure below. The two values highlighted in red were plotted by using the formulae above, so the calculations seem correct because of the strong visual correspondence between the calculated local maxima/minima and those plotted.
If you have any idea as to what's causing the discrepancy in the results given by L&L and those reported here, please feel free to comment.

Another observation: one should note that the formula $\begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$ holds only when the cosine obviously lies in the interval $\left[-1,1\right]$; after some boring calculations, one finds that this happens when $V>v_{20} ~\text{or}~ V<v_{10}$, meaning that when $v_{10}<V<v_{20}$ the derivative of $\cot{\theta}$ does not change sign. This is also why $\cot{\theta}$ may assume all the values between $0$ and $\pi$ in that interval. In the graph below the function $\cot{\theta}$ is set to zero when $v_{10}<V<v_{20}$ for simplicity, because, rigourously speaking, it would also depend on the values of $\theta_{0}$.

close all
clc
v10=18;
v20=22;
v=linspace(v10-3,v20+3,1000000);
costheta0=(v20-v10).*v./(v.^2-v10.*v20);
%theta0=acosd(costheta0);
sintheta0=sqrt(1-costheta0.^2);
ctgtheta=real(((v10+v20)-(v20-v10).*costheta0.^2)./((v10+v20).*costheta0.*sintheta0));
% figure,plot(v,ctgtheta)
% grid on
% xlabel('v')
% ylabel('cot(\theta)')

sq=sqrt((v20+v10)/(3*v10+v20));
vopt=-(v20-v10)/2/sq+1/2/sq*sqrt((v20-v10)^2+4*v10*v20*sq^2); %velocity when cotangent is minimum
vmin=vopt
vmax=(v20-v10)/2/sq+1/2/sq*sqrt((v20-v10)^2+4*v10*v20*sq^2) %velocity when cotangent is minimum
localmaximumcotvalueoftheta=-2*sqrt(1-(v20-v10)/(v10+v20)) %cotangent value of theta at the maximum location
localminimumcotvalueoftheta=2*sqrt(1-(v20-v10)/(v10+v20))
anglemaximumcottheta=180+acotd(-2*sqrt(1-(v20-v10)/(v10+v20))) %angle theta when cotangent is maximum
theta0=acosd((v20-v10).*vopt./(vopt.^2-v10.*v20)) %value of theta0
%ylim([-8 8])

angleminimumcottheta=acotd(2*sqrt(1-(v20-v10)/(v10+v20))) %angle theta when cotangent is minimum
theta0Landau=asind(sin(vopt*(v10+v20)/(vopt^2+v10+v20)))

createfigure(v, ctgtheta)
ylim([-8 8])
plot(vmin,localmaximumcotvalueoftheta,'MarkerSize',5,'Marker','o','LineWidth',5,'LineStyle','none',...
    'Color',[1 0 0]);
plot(vmax,localminimumcotvalueoftheta,'MarkerSize',5,'Marker','o','LineWidth',5,'LineStyle','none',...
    'Color',[1 0 0]);
labelmax=['x=' num2str(vmax) ', y=' num2str(localminimumcotvalueoftheta)];
text(vmax,localminimumcotvalueoftheta,labelmax,'VerticalAlignment','bottom','HorizontalAlignment','center',...
    'FontSize',15,'color',[1 0 0])
labelmin=['x=' num2str(vmin) ', y=' num2str(localmaximumcotvalueoftheta)];
text(vmin,localmaximumcotvalueoftheta,labelmin,'VerticalAlignment','bottom','HorizontalAlignment','center',...
    'FontSize',15,'color',[1 0 0])function createfigure(X1, Y1)
%CREATEFIGURE(X1, Y1)
%  X1:  vector of x data
%  Y1:  vector of y data

%  Auto-generated by MATLAB on 23-Apr-2019 18:27:28

% Create figure
figure1 = figure;

% Create axes
axes1 = axes('Parent',figure1);
hold(axes1,'on');

% Create plot
plot(X1,Y1,'LineWidth',4);

% Create ylabel
ylabel('cot(\theta)','Rotation',0);

% Create xlabel
xlabel('V');

% Uncomment the following line to preserve the Y-limits of the axes
% ylim(axes1,[-8 8]);
box(axes1,'on');
grid(axes1,'on');
% Set the remaining axes properties
set(axes1,'FontSize',30,'XTick',[15 16 17 18 19 20 21 22 23 24 25],'YTick',...
    [-8 -6 -4 -2 0 2 4 6 8]);
end

 

[emaz]

Jeez….Unfortunately, after the formula:
$$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
the calculations are wrong, because I was not focused enough and instead of using the formula above, I mistakenly used
$$ \begin{align} \cos\theta_{0}=\frac{(v_{20}+v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
with a plus sign.
It does not matter (apart from the fact thay I wasted a great amount of time, how embarassing...), since the core of the matter here is to understand whether the solution to the problem has been set up correctly (something which I cast doubt on at this point).

 

[emaz]

I solved it! It would have been much easier if the book had given a different name to the angle $\theta_{0}$. In fact, it is not to be intended as the same angle as the one introduced by the book in prior graphical constructions and problems. Hence, even if the problem is conceptually very simple, this might create confusion.
For the sake of completion, to bring this post to an end, I shall add some details for the solution (also to try and redeem myself from some careless mistakes :) ).
The function we have to analyze is:
$$ \begin{align}\tan{\theta} = \frac {(v_{10}+v_{20})V\sin{\theta_{0}}}{V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }} \nonumber\end{align}$$
or equivalently:
$$ \begin{align}\cot{\theta} = \frac {V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }}{(v_{10}+v_{20})V\sin{\theta_{0}}} \nonumber\end{align}$$ where $\theta_{0} \in \left[0,\pi \right]$, $V \geq 0$.

In order to find the extrema, I took the derivative with respect to $\theta_{0}$ and found the expression:
$$ \begin{align} \frac {\partial\cot{\theta}} {\partial\theta_{0}} = \frac {(-v_{10}+v_{20})V^2-V\cos\theta_{0}\left[V^2-v_{10}v_{20}\right] }{(v_{10}+v_{20})V^2\sin^2\theta_{0}} \nonumber\end{align}$$
By setting the result to 0 one gets: $$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$

One should notice that the formula $\begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$ holds only when the cosine obviously lies in the interval $\left[-1,1\right]$; after some calculations, one finds that this happens when $V \geq v_{20} ~\text{or}~ V\leq v_{10}$, meaning that when $v_{10}<V<v_{20}$ the derivative of $\cot{\theta}$ does not change sign.
Moreover, one could calculate the derivative of the cotangent with respect to $V$ and find the expression:
$$ \begin{align} \frac {\partial\cot{\theta}} {\partial V} = \frac { V^2+v_{10}v_{20} } { (v_{10}+v_{20})V^2\sin\theta_{0} } \nonumber\end{align}$$
which is positive for all values of $V$.
This is why $\cot{\theta}$ may assume all the values between $0$ and $\pi$ when $v_{10}<V<v_{20}$, because $\frac {\partial\cot{\theta}} {\partial\theta_{0}}\neq 0$ and $\frac {\partial\cot{\theta}} {\partial V} \neq 0$ $\forall ~V, \theta_{0}$ in that interval and it is easy to see that if $V$ is kept constant and $\theta_{0}$ is varied between 0 and $\pi$, $\cot\theta$ spans the interval $\left]-\infty,+\infty \right[$; similarly, if $\theta_{0}$ is kept constant and $V$ is varied between 0 and +$\infty$, $\cot \theta$ spans the interval $\left]-\infty,+\infty \right[$.
When $V \leq v_{10}$, it is easy to see that $\cot{\theta}$ has a maximum value. In fact, $\lim_{\theta_{0} \rightarrow 0^+} {\cot(x)} = -\infty$, $\lim_{\theta_{0} \rightarrow \pi^-} {\cot(x)} = -\infty$ and the maximum value of the cotangent is reached when:
$$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
The calculation of the maximum value leads to:
$$ \begin{align} \cot{\theta} &= \frac {V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }}{(v_{10}+v_{20})V\sin{\theta_{0}}}= \nonumber \\
\dots &= \frac{v_{20}-v_{10}}{v_{20}+v_{10}} \frac{ \sin{\theta_{0}} }{\cos{\theta_{0}}}= \dots \nonumber \\
&=-\frac{\sqrt{\left( V^2-v_{10}v_{20}\right)^2-\left(v_{20}-v_{10}\right)^2 V^2}}{\left(v_{10}+v_{20}\right)V } \nonumber \end{align}$$
Then, after transforming the cotangent into a sine, one gets:$$ \begin{align} \sin\theta=\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}} \nonumber\end{align}$$ If we put: $$ \begin{align} \alpha=\sin^{-1}{\left(\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}}\right)} \nonumber\end{align}$$
then, in the interval where $V\leq v_{10}$, we have the following ranges for $\theta$: $\pi-\alpha \leq \theta \leq \pi$.
Similarly, when $V \geq v_{20}$, it is easy to see that $\cot{\theta}$ has a minimum value. In fact, $\lim_{\theta_{0} \rightarrow 0^+} {\cot(x)} = +\infty$, $\lim_{\theta_{0} \rightarrow \pi^-} {\cot(x)} = +\infty$ and the minimum value of the cotangent is reached when $\theta=\alpha$. In this case the ranges for $\theta$ are: $0 \leq \theta \leq \alpha$ (the equality $\theta=0$ is satisfied only when $V \rightarrow +\infty$).
To summarize:

$$ \begin{align} &\text{if}~~ v_{10}<V<v_{20} \rightarrow 0<\theta<\pi \nonumber \\
\nonumber \\
&\text{if}~~ V\leq v_{10} \rightarrow \pi-\alpha \leq \theta \leq \pi \nonumber \\
\nonumber \\
&\text{if}~~ V\geq v_{20} \rightarrow 0\leq\theta\leq\alpha \nonumber\end{align} $$
where $$ \begin{align} \alpha=\sin^{-1}{\left(\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}}\right)} \nonumber\end{align}$$