- #1
wr1015
- 53
- 0
Vectors problem help, please!
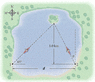
Two canoeists start paddling at the same time and head toward a small island in a lake. Canoeist 1 paddles with a speed of 1.60 m/s at an angle of 45° north of east. Canoeist 2 starts on the opposite shore of the lake, a distance d = 1.59 km due east of canoeist 1.
(a) In what direction relative to north must canoeist 2 paddle to reach the island?? the answer in degrees west of north.
(b) What speed must canoeist 2 have if the two canoes are to arrive at the island at the same time?
Two canoeists start paddling at the same time and head toward a small island in a lake. Canoeist 1 paddles with a speed of 1.60 m/s at an angle of 45° north of east. Canoeist 2 starts on the opposite shore of the lake, a distance d = 1.59 km due east of canoeist 1.
(a) In what direction relative to north must canoeist 2 paddle to reach the island?? the answer in degrees west of north.
(b) What speed must canoeist 2 have if the two canoes are to arrive at the island at the same time?