- #1
- 3,631
- 1,511
A problem I was thinking about when talking about natural circulation in a closed loop in another thread:
What is the velocity of the buoyant plug? The loop is filled with water. There are no viscous forces acting on the plug or in the flow. The flow is assumed incompressible.
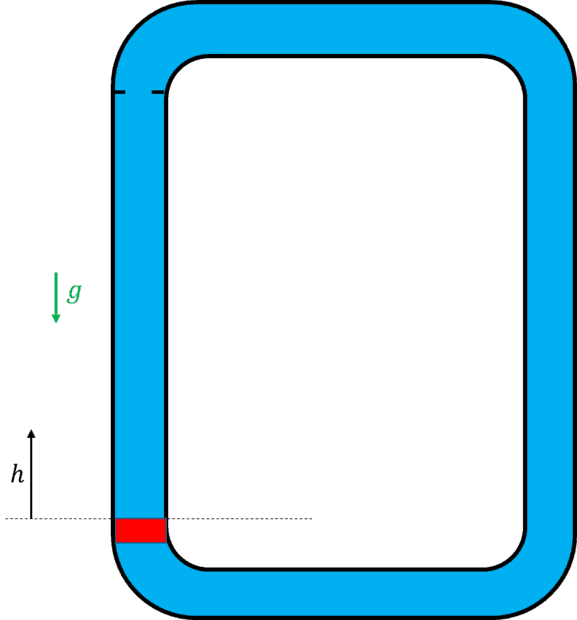
1) Is the buoyant force constant? I was thinking conservation of energy, but does the fact that the fluid is accelerating with the plug effect it?
$$ \int F_b ~dh = m_p g h + \frac{1}{2}m_p v_p^2 + \frac{1}{2}m_w v_p^2$$
with ## v_w = v_p ##
2) I assume its ok to neglect the small change in the fluid center of mass as the plug ascends?
What is the velocity of the buoyant plug? The loop is filled with water. There are no viscous forces acting on the plug or in the flow. The flow is assumed incompressible.
1) Is the buoyant force constant? I was thinking conservation of energy, but does the fact that the fluid is accelerating with the plug effect it?
$$ \int F_b ~dh = m_p g h + \frac{1}{2}m_p v_p^2 + \frac{1}{2}m_w v_p^2$$
with ## v_w = v_p ##
2) I assume its ok to neglect the small change in the fluid center of mass as the plug ascends?