Calculating h in a Venturi Tube

[Metalsonic75]

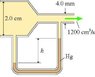
Air flows through this tube at a rate of 1200 cm^3/sec. Assume that air is an ideal fluid.
What is the height h of mercury (in cm) in the right side of the U-tube?

In case the picture doesn't show up, the tube is a Venturi tube. Wide end has diameter of 2cm, narrow diameter is 4 mm, and velocity of the air exiting the tube is 1200 cm^3/sec. The mercury is higher in the u-tube section directly below the narrow segment, and I need to find the height difference of the mercury on the right and left sides.

I've tried using the velocity equations for a venturi tube: v_1 = A_2*sqrt[(2rho*gh)/rho(A_1^2 - A_2^2)] and solving for h. I also tried using the equation p_1 + 0.5rho*v_1^2 = p_1 - rho*gh + 0.5rho(A1/A2)^2*v_1^2 and solving for h.

I'm not getting the right answers. I got something like 6.40cm for the first method, and 8.31cm. To obtain the velocity in the larger part of the tube I used A1v1=A2v2
and got 48 cm^3/sec.

I also have no idea what to do with all of these units. Should I leave all of my measurements in centimeters (2 cm, 1200cm^3/sec, etc) or in meters (0.02m, 12 m^3 sec, etc.) I might be getting the right answer, and be off by a factor of 100. How can I calculate the h?

I appreciate your time.

 

[TSny]

Wide end has diameter of 2cm, narrow diameter is 4 mm, and velocity of the air exiting the tube is 1200 cm^3/sec.

The velocity at the exit is not 1200 cm³/s. Note that the units here do not correspond to speed. 1200 cm³/s is the volume flow rate, Q. Q is the same at any cross-section of the tube if the flow is steady and incompressible. (These are natural assumptions to make for this problem.)

At any cross-section, Q is related to the speed v of the fluid according to Q = Av, where A is the cross-sectional area. This relation is useful for finding v if you know Q.

I've tried using the velocity equations for a venturi tube: v_1 = A_2*sqrt[(2rho*gh)/rho(A_1^2 - A_2^2)] and solving for h.

You can use this equation to find h. However, one of the rhos is the density of air while the other rho is the density of mercury. I leave it to you to figure out which is which.