- #1
Zrpeip
- 4
- 0
Hi everyone, first post.
Just wanted to say I've been using parts of this forum for a long time for help in understanding all kinds of concepts, and have found it immensely helpful over the years. Thank you for all of your contributions!
So, here goes with my hopefully very simple question:
From a practice exam with answer key.
Written: 'What is the value of the voltage U?'
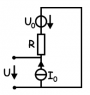
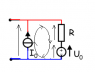
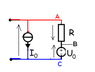
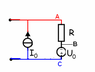
The drawing: a simple closed loop with 3 circuit elements in series (from top to bottom on one side): an ideal voltage source U_0 (positive terminal 'on top'), a resistor R, and an ideal current source I_0 (current emerges 'on top').
The voltage in question U appears across two terminal legs placed above and below the ideal current source, and has the same orientation as the voltage source (i.e. positive terminal 'on top').
I've attached a picture as well.
I used KVL in the main loop (clockwise):
-U_0 + R*I_0 -U = 0
The above equation gave me my solution, or so I thought. U = R*I_0 - U_0.
However, the listed solution is U = R*I_0 + U_0.
I would assume that R*I_0 and U_0, written symbolically as they are in this problem, could never have the same sign (following the KVL loop and polarities).
But I don't feel that I understand how to treat voltages across ideal current sources anyway. So perhaps my problem is there. I would appreciate any explanation of how to approach that in general as well.
I'm still a beginner and make dumb mistakes in circuit analysis all the time and root most of them out eventually, but for whatever reason I'm not getting it here. I think I've overthought it. Thanks in advance!
Just wanted to say I've been using parts of this forum for a long time for help in understanding all kinds of concepts, and have found it immensely helpful over the years. Thank you for all of your contributions!
So, here goes with my hopefully very simple question:
Homework Statement
From a practice exam with answer key.
Written: 'What is the value of the voltage U?'
The drawing: a simple closed loop with 3 circuit elements in series (from top to bottom on one side): an ideal voltage source U_0 (positive terminal 'on top'), a resistor R, and an ideal current source I_0 (current emerges 'on top').
The voltage in question U appears across two terminal legs placed above and below the ideal current source, and has the same orientation as the voltage source (i.e. positive terminal 'on top').
I've attached a picture as well.
Homework Equations
I used KVL in the main loop (clockwise):
-U_0 + R*I_0 -U = 0
The Attempt at a Solution
The above equation gave me my solution, or so I thought. U = R*I_0 - U_0.
However, the listed solution is U = R*I_0 + U_0.
I would assume that R*I_0 and U_0, written symbolically as they are in this problem, could never have the same sign (following the KVL loop and polarities).
But I don't feel that I understand how to treat voltages across ideal current sources anyway. So perhaps my problem is there. I would appreciate any explanation of how to approach that in general as well.
I'm still a beginner and make dumb mistakes in circuit analysis all the time and root most of them out eventually, but for whatever reason I'm not getting it here. I think I've overthought it. Thanks in advance!