- #1
nejla
- 6
- 0
Dear all,
I do really need your help.
I'd like to find the volume contained between a sphere (x^2+y^2+z^2=r^2) , plane1 (ax+by+cz+d=0), and plane2 (z-h=0).
Would you please check what I've done till now?
From the sphere and plane1 equations I got:
x1=sqrt*(r^2-y^2-z^2)
x2=d/a-(b/a)y-(c/a)z
Then, by assuming that x1=x2 (as the sphere and plane1 intersect), I derived two equations: one for y1 and one for y2 as follow:
y1=f(z)
y2=g(z)
Also, by assuming y1=y2, I got:
z1=M (a constant value)
z2=N (a constant value)
Now, let assume z1<h<z2
So, to derive the volume I thought that I can run three integrals as bellow:
A=int(1,x,x1..x2)
B=int(A,y,y1..y2)
volume = int(B,z,h..z2)
Am I right? Would you please let me know that what I am doing is right or not?
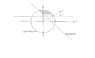
I also drew a simple picture. The shaded area represents the portion of the sphere that I am looking for its volume.
Thanks in advance,
Nejla
I do really need your help.
I'd like to find the volume contained between a sphere (x^2+y^2+z^2=r^2) , plane1 (ax+by+cz+d=0), and plane2 (z-h=0).
Would you please check what I've done till now?
From the sphere and plane1 equations I got:
x1=sqrt*(r^2-y^2-z^2)
x2=d/a-(b/a)y-(c/a)z
Then, by assuming that x1=x2 (as the sphere and plane1 intersect), I derived two equations: one for y1 and one for y2 as follow:
y1=f(z)
y2=g(z)
Also, by assuming y1=y2, I got:
z1=M (a constant value)
z2=N (a constant value)
Now, let assume z1<h<z2
So, to derive the volume I thought that I can run three integrals as bellow:
A=int(1,x,x1..x2)
B=int(A,y,y1..y2)
volume = int(B,z,h..z2)
Am I right? Would you please let me know that what I am doing is right or not?
I also drew a simple picture. The shaded area represents the portion of the sphere that I am looking for its volume.
Thanks in advance,
Nejla
Attachments
Last edited: