- #1
Guest432
- 48
- 2
I am trying to gain some understanding from this article regarding deriving the volume of an arbitrary pyramid.
"An arbitrary pyramid has a single cross-sectional shape whose lengths scale linearly with height. Therefore, the area of a cross section scales quadratically with height, decreasing from
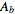 at the base ([PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline5.gif) to 0 at the apex (assumed to lie at a height [PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline6.gif). The area at a height http://mathworld.wolfram.com/images/equations/Pyramid/Inline7.gif above the base is therefore given by"
at the base ([PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline5.gif) to 0 at the apex (assumed to lie at a height [PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline6.gif). The area at a height http://mathworld.wolfram.com/images/equations/Pyramid/Inline7.gif above the base is therefore given by"
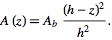
Can you describe this to me mathematically but easily?
"An arbitrary pyramid has a single cross-sectional shape whose lengths scale linearly with height. Therefore, the area of a cross section scales quadratically with height, decreasing from
Can you describe this to me mathematically but easily?
Last edited by a moderator: