- #1
chawki
- 506
- 0
Homework Statement
The volume of a pyramid can be evaluated by using the equation V=1/3*A*h where h is
the height of the pyramid and A is the area of the base of the pyramid. The problem is
to design such a triangular pyramid where the volume is V = 72 cm3 and the height is
h = 12 cm. The base of the pyramid is a rectangular isosceles triangle.
Homework Equations
a) Determine the area of the base of the pyramid. Pay attention to the unit of your answer.
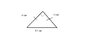
b) Draw a picture of the base triangle of the pyramid in a proper scale
The Attempt at a Solution
a)
V=1/3*A*h
A=72/(12/3)=18cm2
b) A = 18 = b*y
b=y
so: 18=2*b => b = 9cm

 my mistake, i thought it's a pyramid with 4 faces..
my mistake, i thought it's a pyramid with 4 faces..