- #1
kent davidge
- 933
- 56
Homework Statement
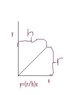
Find the volume of a right circular cone with height h and base radius r.
Homework Equations
The Attempt at a Solution
I've chosen the case where y = x = r = h. Then, I solve the integral in the image above and I got the book's answer. But is it actually correct?