- #1
Gh778
- 421
- 0
Hi,
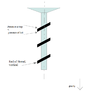
The weight on Earth is F = m*g with g = G*M/(r+h)² with G = 6,6742 e-11, M mass of Earth and r the altitude or radius of Earth and h local altitude. M = 5,9736e24 kg. r = 6371000 m.
With 2 masses M1 and M2 of 1kg each at altitude h = 0 m, the weight is g*2 = 2*9.82245719295718826387 = 19.64491438591437652774 N
If we turn these masses (radius = 1 m, 2 masses are diametrically opposed) for have h = -1 m for one mass and h = +1 m, now the total weight is 9.82245410946797767206 + 9.82246027644785082081 = 19.64491438591582849287 N
The difference is + 1.45196513e-12 N sure this difference is at only one point, we need to integrate for have the total weight but it can't be the same at h = 0 m.
Like masses are always the same, I think centripetal forces don't change. And we can accelerate/deccelerate masses when h = 0 m. The masses can always turn (if friction is very low), the support see more weight.
So turn 2 masses add weight for the support ?
The weight on Earth is F = m*g with g = G*M/(r+h)² with G = 6,6742 e-11, M mass of Earth and r the altitude or radius of Earth and h local altitude. M = 5,9736e24 kg. r = 6371000 m.
With 2 masses M1 and M2 of 1kg each at altitude h = 0 m, the weight is g*2 = 2*9.82245719295718826387 = 19.64491438591437652774 N
If we turn these masses (radius = 1 m, 2 masses are diametrically opposed) for have h = -1 m for one mass and h = +1 m, now the total weight is 9.82245410946797767206 + 9.82246027644785082081 = 19.64491438591582849287 N
The difference is + 1.45196513e-12 N sure this difference is at only one point, we need to integrate for have the total weight but it can't be the same at h = 0 m.
Like masses are always the same, I think centripetal forces don't change. And we can accelerate/deccelerate masses when h = 0 m. The masses can always turn (if friction is very low), the support see more weight.
So turn 2 masses add weight for the support ?