How does rotation affect weight changes?

[Gh778]

Hi,

The weight on Earth is F = m*g with g = G*M/(r+h)² with G = 6,6742 e-11, M mass of Earth and r the altitude or radius of Earth and h local altitude. M = 5,9736e24 kg. r = 6371000 m.

With 2 masses M1 and M2 of 1kg each at altitude h = 0 m, the weight is g*2 = 2*9.82245719295718826387 = 19.64491438591437652774 N

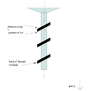
If we turn these masses (radius = 1 m, 2 masses are diametrically opposed) for have h = -1 m for one mass and h = +1 m, now the total weight is 9.82245410946797767206 + 9.82246027644785082081 = 19.64491438591582849287 N

The difference is + 1.45196513e-12 N sure this difference is at only one point, we need to integrate for have the total weight but it can't be the same at h = 0 m.

Like masses are always the same, I think centripetal forces don't change. And we can accelerate/deccelerate masses when h = 0 m. The masses can always turn (if friction is very low), the support see more weight.

So turn 2 masses add weight for the support ?

 

[mfb]

If your system with the masses is rotating, the support will see a small oscillation of the required force (probably too small to be measured currently).

There is another effect: A horizontal distance of 1m changes the distance to the center of the earth, too.
$$r=\sqrt{r_{earth}^2 + 1m^2} \approx r_{earth}+\frac{1m^2}{2r_{earth}}$$
This lowers the force for the horizontal position.

 

[willem2]

There's no way to measure such a small effect. The gravitational constant is know only to abouat 1 part in 10^5. The effect could very well have the opposite effect if the density of the ground is a bit lower than average, or you're at the bottom of a heavy building.

 

[Gh778]

There is another effect: A horizontal distance of 1m changes the distance to the center of the earth, too.

You're right ! a very small effect compared to the start very small effect :)

The gravitational constant is know only to abouat 1 part in 10^5.

Sure, we can't measure such small difference but calculations can, no ?

The effect could very well have the opposite effect if the density of the ground is a bit lower than average, or you're at the bottom of a heavy building.

I don't understand, could you explain ?

Edit: I add the integrate

p = 2*G*M/(R+x)² with x the local altitude (h)

The difference of weight is:

Δp = 2*G*M/R² - 2*G*M*(1/(R²-h²))

For my example Δp = 4.83 e-13 N

 

[K^2]

In other words, weight of an object in non-uniform field depends on object's geometry. Well, yes... So what?

 

[Gh778]

It's strange (for me), never see it before. We can move down 2 masses M1/M2 when they rotate and move up 2 masses when they're fixed. The sum of energy is not 0 (for me). I thought of centripetal force but it's only mass in equation not weight. And acceleration/deceleration can be done when h=0. Maybe something consume energy, where ?

 

[willem2]

The magnitude of your extra force is mMG /(r+h)^2 + mMG/(r-h)^2 - 2m MG/r^2.

Bringing this under a common denominator, we get:

$$m M G \frac {- 2 h^4 - 2 r^2 h^2} {(r^2) (r+h)^2(r-h)^2} \approx 2 m M G \frac {h^2 } {r^4}$$

because of this r^4 in the denominator, the effect is much bigger for a smaller object, than for a larger object. for an 1 m radius ball of rock weighing 10^4 kg, at a distance of 2m, the effect is 8.3*10^(-8) h^2. For the Earth as a whole it's only 4.8*10^(-13) h^2.
This means that your effect is going to be completely swamped by the tidal effects, from even small masses in the neighbourhood.

 

[D H]

There's no way to measure such a small effect. The gravitational constant is know only to abouat 1 part in 10^5. The effect could very well have the opposite effect if the density of the ground is a bit lower than average, or you're at the bottom of a heavy building.

G is known to one part in 10⁴, not 10⁵. http://physics.nist.gov/cgi-bin/cuu/Value?bg

That is irrelevant, however. It is G*M that counts, and for the Earth this product is known to nine or ten places. In fact, it what counts even more is what an accelerometer can measure, and that's getting up to 12 or more places nowadays.

$$m M G \frac {- 2 h^4 - 2 r^2 h^2} {(r^2) (r+h)^2(r-h)^2} \approx 2 m M G \frac {h^2 } {r^4}$$

That should be $mMG \frac {6r^2h^2-2h^4} {r^2(r+h)^2(r-h)^2} \approx 6mMG \frac {h^2} {r^4}$. A factor of six instead of two; otherwise the same.

This means that your effect is going to be completely swamped by the tidal effects, from even small masses in the neighbourhood.

That's not true. To compare apples to apples you need to compute the difference between the tidal effects in the two orientations. This difference is essentially zero.
Here's a MEMS device that measures exactly what the OP is talking about: http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=ASMECP002009043857000937000001&idtype=cvips&gifs=yes&ref=no

Edit
Well, not quite what the OP is talking about. The OP happened to pick the two orientations in which there is no gravity gradient torque.

 

[K^2]

I think he's just surprised that there's a difference, which is related to the gradient torque, and more generally, he seems to be inching towards the concept of tidal stretching.

 

[Hassan2]

Yes if the two equal mass connected with a uniform bar is put in the orbit of Earth, it would be aligned so that the bar would be pointing at Earth.

 

[Gh778]

To compare apples to apples you need to compute the difference between the tidal effects in the two orientations. This difference is essentially zero.

Could you explain more please ?

 

[willem2]

Could you explain more please ?

I don't get that either. The formula I computed and DH corrected shows that the effect for the Earth is very small, but that the effect for a mass a few metres away is much larger.

This can be, because for close objects, one of the masses can be substantially closer to the object than the other, so there can be an extra attraction on the same order of magnitude as the actual gravitational attraction between the masses and the object.

For the earth, This setup makes the gravitational force, proportional to 1/r^2 but also the tidal gradient, proportional to 1/r^3 vanish, leaving only a very small term, proportional to 1/r^4

 

[Gh778]

Ok like that.

For the sum of energy, if we move down the support with 2 masses M1/M2 in rotation, we move down more weight than we move up if masses M1/M2 are stop. Where is the difference of energy ?

 

[mfb]

You need energy to rotate your setup (or can get energy in the other direction). And this energy depends on the height of the setup.

>> You're right ! a very small effect compared to the start very small effect :)
I think they have the same order of magnitude (mMgh^2/r^4).

 

[D H]

Gh778, you have stumbled across an interesting fact, that center of gravity and center of mass are not the same thing.

There's an error in your calculation of the gravitational force for the horizontal orientation of your apparatus. The force is not 2GmM/R². The distance between each of the point masses and the center of the Earth is slightly more than R, and the gravitational forces acting on the two masses are not parallel.

Rather than correct that, it is useful to generalize this apparatus so we can look at any orientation rather than just vertical versus horizontal. This generalized apparatus comprises two point masses that are connected via a rigid, massless rod. The apparatus is attached at the center of mass to a pivot such that connecting rod is normal to the axis of rotation.

Assumptions:
1. The apparatus is subject to Earth gravity only.
2. The Earth's gravitation field is that of a point mass.

Conventions:
- $m$ - The mass of each point mass.
- $M$ - The mass of the Earth.
- $h$ - The half-length of the connecting rod.
- $R$ - The distance from the pivot point to the center of the Earth.
- $\hat x$ - Points vertically, +x is downward.
- $\hat z$ - The axis of rotation (horizontal).
- $\hat y$ - Completes a right hand system.
- $\theta$ - The displacement of the apparatus from vertical.

The net gravitational force on the apparatus is
$$\begin{aligned}F_g &= GmM \left( \frac{(R - h\cos\theta)\,\hat x - h\sin\theta\,\hat y} {||(R - h\cos\theta)\,\hat x - h\sin\theta\,\hat y||^3} + \frac{(R + h\cos\theta)\,\hat x + h\sin\theta\,\hat y} {||(R + h\cos\theta)\,\hat x + h\sin\theta\,\hat y||^3} \right) \\ & \approx \frac{GmM}{R^2} \left( ( 2 + 3 (3\cos^2\theta-1) (h/R)^2 )\,\hat x - 6 \sin\theta\cos\theta (h/R)^2\, \hat y \right) \end{aligned}$$

There is also a torque on the apparatus. This gravity gradient torque is
$$\begin{aligned}\tau_{gg} &= GmMh \left( (\cos\theta\,\hat x + \sin\theta\,\hat y) \times \frac{(R - h\cos\theta)\,\hat x - h\sin\theta\,\hat y} {||(R - h\cos\theta)\,\hat x - h\sin\theta\,\hat y||^3} + (-\cos\theta\,\hat x - \sin\theta\,\hat y) \times \frac{(R + h\cos\theta)\,\hat x + h\sin\theta\,\hat y} {||(R + h\cos\theta)\,\hat x + h\sin\theta\,\hat y||^3} \right) \\ &\approx -GmM\frac{6\sin\theta\cos\theta h^2}{R^3} \end{aligned}$$

This gravity gradient torque is measurable. Due to the 1/R³ nature of this torque, it is quite sensitive to gravitational anomalies such as deposits of ore or oil. Gravimeters are one of the tools that mining companies and oil companies use to find the next place to dig or drill.

 

[Gh778]

Great D H for yours equations ! and thanks

1/ If we accelerate/decelerate masses M1/M2 when they are at horizontal position, does the kinetics energy change with different altitude of the apparatus ? (Without friction). Example: altitude = 100 m, we accelerate masses when they are at horizontal position, move down the apparatus at altitude of 0 m and when masses are at horizontal position recover kinetics energy.

2/ Does centripetal forces change the weight or the torque in yours equations ?

Edit:

3/ The net gravitationnal force is in R$^{4}$ but the torque is in R$^{3}$, how the sum of energy is 0 ?

 

[Gh778]

With a ring (full ring, ot full torus), the torque exist always ? If not, what's compensated the net gravitationnal force ?

Edit:

I have calculate with 2 cases, masses at the same point and masses in vertical fixed position (never rotate). All the system move down of 100 m.

A/ If masses are in same point, I move down for 100 m, the energy is 2mGMH/100*(1/(r-100)-1/(R)) = +1964.52227397479936678121 J, with H = 100 m the height to move down

B/ Now I move up one mass of 1 m and move down one mass of 1 m, this give energy: m*G*M/1*(-1/(R+1)+1/R+1/(R-1)-1/R) = +19.64491438591486051612 J

Now I move down all apparatus, this give: m*G*M*H/100*(1/(R+1-99)-1/(R+1)+1/(R-1-101)-1/(R-1)) = +1964.52228322584998078757J

Now I move up one mass and move down other mass of 1 m for have the masses at the same place than A this need: m*G*M/1*((1/(R-99)-1/(R-100))-(1/(R-101)-1/(R-100))) = -19.64553109842213051418 J

The difference is 0.00061671236206892742 J where my calculations are false ?

 

[mfb]

With a ring, you would have to integrate over the angle, and the result is 0.
The same can be seen just from symmetry of the ring.

>> B/ Now I move up one mass of 1 m and move down one mass of 1 m, this give energy [...] +19.64491438591486051612 J
This is way too large (and roughly equivalent to the energy you get from just moving one mass by one meter).
You move your masses down by 100m two times?

In general, you should check your formulas. One example: (R-99m) just appears in the last expression. But how did the mass come to this position?
"1/(R+1-99)-1/(R+1)" <- this is a movement by 99 meters, not 100

Anyway: You just go from one potential energy to another. By construction, you have to arrive at 0 if you do that in a circle. (a-b)+(b-c)+(c-a)=0.

 

[nicu]

G is an imitation of g and his formula and value are very doubtful...

 

[Gh778]

I have corrected

2*m*G*M*H/100*(1/(R-100)-1/(R)) = 1964.52227397479936678121

compared to

m*G*M/1*(-1/(R+1)+1/R-1/(R-1)+1/R) = +3.08348993657429924912e-6
m*G*M*H/100*(1/(R-99)-1/(R+1)+1/(R-101)-1/(R-1)) = 1964.52227397494456785185

m*G*M/1*((1/(R-99)-1/(R-100))+(1/(R-101)-1/(R-100))) = -0.08363513764493721675e-6

The sum is :

1964.52227397479936678121-3.08348993657429924912e-6-1964.52227397494456785185+3.08363513764493721675e-6 = 1e-27 it's ok, the sum is 0.

3/ The net gravitationnal force is in R 4 but the torque is in R 3 , how the sum of energy is 0 ?

How the sum can be to 0 ?

 

[Gh778]

I have thought about something I don't understand. When a screw is in water with bottom thread end with vertical surface. The torque on the bottom surface is canceled all along the thread with a differencial of pressure (up/down surface of the thread). With the pressure of water = f(h) it's ok, all torque are canceled, but now with pressure = f(h,Δh²) why the bottom torque is not greater than the differencial torque ? The difference is not big but must be to 0 I think ?

NB. We are for example on Earth with gravity = 9.81 m/s². The screw can only turn.

 

[Gh778]

All is fine I understand the problem.

But for this thread I will calcultate if the torque is 0 :

A circular thread (can only turn) in sandwich between 2 circular fixed thread. Up and down small film of water. See the drawing. The thread has only film of water up and down.Normally, this thread don't turn because the height of water is the same. But really, one side is more far from Earth (the up side). This give a torque ?

 

[Gh778]

I drew the developpant of the helicoid (thread). This helicoid is in a sandwich between 2 fixed helicoids. Only film of water Up and Down surfaces.

The down torque = T1 = Radius_of_helicoid * Down_surface * density_of_water * height * Gt * Mt * ( g + (1/(R+250) - 1/R ) )

The up torque = T2 = Radius_of_helicoid * Up_surface * density_of_water * height * Gt * Mt * ( g + (1/(R+350) - 1/(R+100) ) )

With:
g = 9.81
Mt = Mass of Earth
Gt = Gravitational constant
Up_surface = Down _surface
k = Radius_of_helicoid * Down_surface * density_of_water * height * Gt * Mt

T1 = k * ( g + (1/(R+250) - 1/R ) ) = 9.8099999999938410347 * k

T2 = k * ( g + (1/(R+350) - 1/(R+100) ) = 9.80999999999384122804 * k

There is a little difference ?

 

[Gh778]

I find the problem, the force is perpendiculary to the surface and movement.

Another question is with a fixed column of water with a fixed mass under it. Like the mass is more at left, the pressure at left in the column is higher than at right. The water move inside the column ? Or another force balance this ? (No other gravity, only mass M and water). Mass of M is 100 or higher than mass of water for example, because there are forces in water alone, the up of water attrack the down, idem for the sides, maybe already a movement in water alone.