- #1
Trying2Learn
- 373
- 57
- TL;DR Summary
- A question about the order of Euler angles
Good Morning
Suppose, for the sake of this question, the following Euler rotations for a gyroscope)
I am trying to rationalize the order of the rotations in this problem (but, more importantly, in the next one).
I can look at the top-body itself and justify, in my head, that the SPIN is the last one: it is the local body frame.
But how can I know that the precession happens before the nutation?
Perhaps it is best to leave the top alone and go to the issue I face...
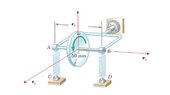
Consider the attached schematic of an inertial guidance system.
(notice that this list is NOT ordered)
Now, I KNOW that I can jump right to the equation for steady precession, align the axes and compute the result.
Moment = J3-disk * (precession_rate * spin_rate)
I can do that easily, knowing the equation
But I am trying to redevelop the equations from scratch.
I can justify that the last rotation is the spin of the disk (just like the top: it is the body frame)
But I cannot seem to justify which one is first, by looking at the problem: the yaw about 3 or the nutation about 2
The order matters!
I know what the answer SHOULD. This order, first to last:
But I am unable to explain why.
(I mean, to be honest, even with the spinning top, it seems that the first rotation, the precession, does not do much. The nutation, leaning over, does more. So I would have been inclinded --- in my stupidity of learning -- to model the nutation first. In other words, for an axisymmetric gyroscope, what gave the early engineers the idea to model the precession first? I would have done the nutation because I can see that.)
Suppose, for the sake of this question, the following Euler rotations for a gyroscope)
- A precession about the vertical 3-axis (like with a top, going around a vertical)
- Then, a nutation (a leaning over) about the 1-axis
- Then, back to the spin itself of the top body about the local body 3-axis
I am trying to rationalize the order of the rotations in this problem (but, more importantly, in the next one).
I can look at the top-body itself and justify, in my head, that the SPIN is the last one: it is the local body frame.
But how can I know that the precession happens before the nutation?
Perhaps it is best to leave the top alone and go to the issue I face...
Consider the attached schematic of an inertial guidance system.
(notice that this list is NOT ordered)
- The disk spins about the local 2-axis,
- The airplane yaws about the vertical 3-axis
- This causes moments (1-axis) and defelections of the spring sensors
Now, I KNOW that I can jump right to the equation for steady precession, align the axes and compute the result.
Moment = J3-disk * (precession_rate * spin_rate)
I can do that easily, knowing the equation
But I am trying to redevelop the equations from scratch.
I can justify that the last rotation is the spin of the disk (just like the top: it is the body frame)
But I cannot seem to justify which one is first, by looking at the problem: the yaw about 3 or the nutation about 2
The order matters!
I know what the answer SHOULD. This order, first to last:
- The yaw about the vertical axis must be the first one.
- Then, the one that brings about the nutation of the disk must be the second: about the 1-axis
- Then, the spin is last
But I am unable to explain why.
(I mean, to be honest, even with the spinning top, it seems that the first rotation, the precession, does not do much. The nutation, leaning over, does more. So I would have been inclinded --- in my stupidity of learning -- to model the nutation first. In other words, for an axisymmetric gyroscope, what gave the early engineers the idea to model the precession first? I would have done the nutation because I can see that.)
Attachments
Last edited: