What is the derivative of 4x(16-x^2)^0.5?

[Tiiba]

I did this three times, and always come up with utter nonsense.

What is the derivative of 4x(16-x^2)^0.5?
(Root of (16 minus x-squared) by 4x.) What are its zilches? How did you calculate that?



This derivative is part of the solution to this problem: "What are the dimentions of the largest rectangle (by area) inscribable in a circle with radius 4?"

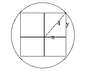
I drew the circle and the square (see attachment), divided the square into four parts, drew a diagonal through one, and called it a hypotenuse, which is equal to 4. X and y are the sides of the mini squares. A = 4xy (since there are 4 mini-squares). Then I used Pythagoras to come up with that equation above. But I can't differentiate it now...

The final answer is supposed to be 32 square units.

 

[matt grime]

you can differentiate it, just keep trying, or you could make your life easier: the maximizing the area is the same as maximizing the square of the area.

 

[homology]

What is the derivative of 4x(16-x^2)^0.5?
(Root of (16 minus x-squared) by 4x.) What are its zilches? How did you calculate that?

Use the product rule and chain rule. I'll get you started:

(d/dx)(4x(16-x^2)^0.5)=4((16-x^2)^0.5)+(4x)(...

As for the zeros, the only important one is 2(2)^.5

This derivative is part of the solution to this problem: "What are the dimentions of the largest rectangle (by area) inscribable in a circle with radius 4?"

matt grime is right, it ends up being a square, but you should start with a rectangle to prove it to yourself.

I drew the circle and the square (see attachment), divided the square into four parts, drew a diagonal through one, and called it a hypotenuse, which is equal to 4. X and y are the sides of the mini squares. A = 4xy (since there are 4 mini-squares). Then I used Pythagoras to come up with that equation above. But I can't differentiate it now...

Sure you can, finish the above differentiation, simplify and then find a root that makes sense in this problem. Use the root to find y and then you'll know the area (which is, as you stated, 32 square units).

Good Luck,

Kevin

 

[Tiiba]

(d/dx)(4x(16-x^2)^0.5)=4((16-x^2)^0.5)+(4x)(...

(d/dx)(4x(16-x^2)^0.5)=4((16-x^2)^0.5) - (4x^2)(16-x^2)^.5 =

-4x^2
-------------- + 4sqrt(16-x^2) = 0;
sqrt(16-x^2)

4x^2
-------------- = 4sqrt(16-x^2) = 0;
sqrt(16-x^2)

4x^2 = 4(16-x^2)

x^2 = 16 - x^2

0 = 16 :yuck:

BTW, this means x = sqrt(16-x^2), which is y.
So x=y, and if this is a square, that's perfectly true.

So there you have it: a full mathematical proof that 0=16.

 

[homology]

(d/dx)(4x(16-x^2)^0.5)=4((16-x^2)^0.5) - (4x^2)(16-x^2)^.5 =

-4x^2
-------------- + 4sqrt(16-x^2) = 0;
sqrt(16-x^2)

The above is good

4x^2 = 4(16-x^2)

x^2 = 16 - x^2

This is bad. "add" x^2 to both sides to get 2(x^2)=16 which yields x=2sqrt(2) and not 0=16

So there you have it: a full mathematical proof that 0=16.

So there you have it: a full mathematical proof that you can't add


Cheers,

Kevin

 

[Tiiba]

You needed calculus to prove THAT?

God, I'm sure glad I'm not studying arithmetic any more.

 

[dedaNoe]

10 = 2 really
I mean:

10₂=2₁₀

1*2^1+0*2^0=2*10^0