What is the tension in the lower cord?

[quick02si]

Hello I really need help I hope someone can help me. Thank You in advance.
The problem reads.
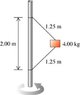
The 4.00-kg block in the figure is attached to a vertical rod by means of two strings. When the system rotates about the axis of the rod, the strings are extended as shown in the diagram and the tension in the upper string is 80.0 N.
1.What is the tension in the lower cord?
2.How many revolutions per minute does the system make?
3.Find the number of revolutions per minute at which the lower cord just goes slack.


Thank You again.

 

[Sirus]

Please show us what you have done so far and where you are stuck. Remember to always begin with a free-body diagram.

 

[quick02si]

On this problem I do thr freebody diagram but i can't determine how to find the angle for the lower cord. At first i though that the 2 tensions would be equal but aparently that is incorrect.

 

[Sirus]

Finding the angle is a good idea. You should be able to create two right-angle triangles with two known side lengths and find the angle (you know the hypothenus is 1.25 m, what is the other side you know?).

 

[quick02si]

Ok I used the Phythagorean Theorem a^2+b^2=c^2: 1+b^2=1.25^2; b=.75. Them I found the angle within the triangle using Sine, which is opposite over hypotnuse. .75/1.25 and the take the inverse of sine. The angle i got was 53.1. I then set up the force in the y direction: T_1(the tension in the top)sin53.1-T_2(tension of the bottom cord)sin(53.1).
T_1sin(53.1)-T_2sin(53.1)=0; T_1sin(53.1)=T_2sin(53.1); so T_1=T_2. But when i put the answer of 80.0N into the program it says that's incorrect. Am i doing this right.
Thank You.

 

[quick02si]

Ok I found the mistake I made. I forgot to subtract the weight. The answer is 31.N. Now I'm going to try the next ones. Thanks for your help.

 

[Sirus]

The two tensions cannot be equal in magnitude since the bottom string does not counter the effect of gravity. Try setting up a force vector diagram using all the forces acting on the body. You should be able to solve for the bottom force.

 

[quick02si]

Ok for part b since i have the radius i found the circumference which is the total distance in one revolution. But how can i get the time. Or what would be the next step in solving the problem.

 

[Sirus]

In order to do part b you need to complete part a. Try vector addition as I explained above.

 

[Sirus]

A little more detail: there is a net force in the horizontal plane (the centripetal force) because the object is in circular motion, but the object does not move vertically. Think about what that tells you about the vertical components of the tensions and how that can help you find part a.

 

[quick02si]

I did finish part a. I said that you for your help in reply #6. The answer was 31N and the reason i had gotten it wrong was because i forgot about the weight.

 

[Sirus]

Oh sorry, I didn't see that one because our posts collided! For part b, do you know the formula for centripetal force as a function of tangential velocity?

 

[quick02si]

Yea when I posted you posted like a milli second right after me. Ok so the i would use one of the kinematic equations to find the velocity.

 

[quick02si]

No i don't know the equation for centripetal force. Can you give it to me please.

 

[Sirus]

I'm not sure how they expect you to do this question without this formula, but anyways,
$$F_{c}=\frac{mv^{2}}{r}$$
You should be able to get part b using that. For part c, use the horizontal components of the tension forces.

 

[quick02si]

Do I use kinematics to find the velocity?

 

[Sirus]

No. Can you find a way to use the centripetal force formula I just posted to find the velocity?