- #1
qqchan
- 14
- 0
Homework Statement
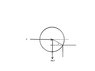
A person pushing horizontally a uniformly-loaded 45.2 kg wheelbarrow is attempting to get it over a horizontal step. The maximum horizontal force that person could apply is F = 410 N. What is the maximum height of the step, as a fraction of the wheel's radius, the person could get the wheelbarrow over? Assume that the height of the step is h=nR.
Homework Equations
τ=Fr
F = mg
The Attempt at a Solution
Calculating the wheelbarrow at the edge of step.
hence
Fr = mg
and I'm stuck here of how to apporach on to the next step