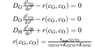- #1
baseball1234
- 3
- 0
Hi, I have the attached diffusion based equations I am looking to solve, however I am unsure about how to implement. I have solved similar equations before, with a simplified r(cG,cO) using the explicit finite difference method and it worked fine. However, I am wondering if that would be OK for this set of equations. I read that people used shooting method to solve these, but I am unfamiliar with this method. Can I also use the differential equation solvers in MATLAB to do this? Thanks.