- #1
kostoglotov
- 234
- 6
I'm almost there in terms of understanding it, but I need to go beyond the text.
Here is the example problem:
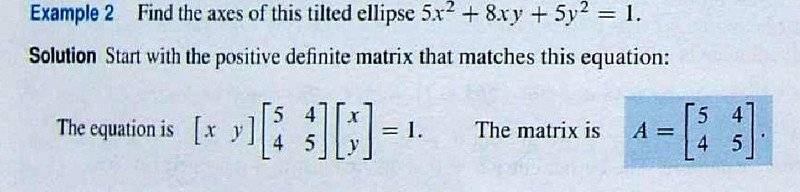
imgur link: http://i.imgur.com/UMj55tF.jpg
I can see that where we have [itex]1 = \vec{x}^T A \vec{x} = \lambda \vec{x}^T \vec{x}[/itex] that [itex]1=\lambda \vec{x}^T \vec{x} = \lambda ||\vec{x}||^2[/itex]
so [tex]||\vec{x}|| = \frac{1}{\sqrt{\lambda}}[/tex]
and I understand that the length of the vector [itex]||\vec{x}||[/itex] will have min and max values when pointing along the minor and major axis'.
What I cannot prove to myself, or see the reason behind, is why the eigenvectors that you would solve for would be pointing in the direction of the minor and major axis'. Why is that? What is the reason for that?
Here is the example problem:
imgur link: http://i.imgur.com/UMj55tF.jpg
I can see that where we have [itex]1 = \vec{x}^T A \vec{x} = \lambda \vec{x}^T \vec{x}[/itex] that [itex]1=\lambda \vec{x}^T \vec{x} = \lambda ||\vec{x}||^2[/itex]
so [tex]||\vec{x}|| = \frac{1}{\sqrt{\lambda}}[/tex]
and I understand that the length of the vector [itex]||\vec{x}||[/itex] will have min and max values when pointing along the minor and major axis'.
What I cannot prove to myself, or see the reason behind, is why the eigenvectors that you would solve for would be pointing in the direction of the minor and major axis'. Why is that? What is the reason for that?