- #1
Fernsanz
- 57
- 0
Hello everyone.
There is a question I have been thinking about for a time. Let's state it the easy way:
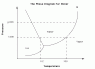
Let's suppose my room is a closed system with constant pressure (1 atm) and temperature (standard 25º C). Under these conditions, if I put a container with water in my room, it will end up empty because water have evaporated. But according to the phase diagram of water, water vapor should not exists as an equilibrium state at those conditions. So, what is wrong?
I understand evaporation (I know the difference with boiling) as a surface phonemenon, but once the system reachs the equilibrium, the water should be liquid as indicated by the phase diagram.
¿Suggestions?
Thanks.
There is a question I have been thinking about for a time. Let's state it the easy way:
Let's suppose my room is a closed system with constant pressure (1 atm) and temperature (standard 25º C). Under these conditions, if I put a container with water in my room, it will end up empty because water have evaporated. But according to the phase diagram of water, water vapor should not exists as an equilibrium state at those conditions. So, what is wrong?
I understand evaporation (I know the difference with boiling) as a surface phonemenon, but once the system reachs the equilibrium, the water should be liquid as indicated by the phase diagram.
¿Suggestions?
Thanks.