Why is h Not Known as Wien's Constant? | Explanation

[AVentura]

TL;DR Summary

it seems he had $h\nu$ first

Could someone please help me understand why $h$ isn't known as Wien's constant?

In his "approximation":

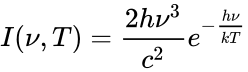
it just looks like he used the wrong distribution function (Maxwell-Boltzmann) with $h\nu$ correctly for energy

And why is the correct distribution function

$$ \frac 1 {e^{\frac E {kT} }-1}$$

Named Bose-Einstein when Planck used it correctly first?

Thank you

 

[PeterDonis]

Names for physical quantities or equations seldom reflect the person who actually first discovered them or used them correctly.

 

[Klystron]

While learning detail about the latest SI units, I encountered a related effort toward replacing proper names for theories with simple (common) descriptors.

Several difficulties with removing and/or replacing proper names:

1. Tradition and concomitant resistance to change; particularly in previously published work.
2. Convention and credit.
3. Brevity and convenience. For example, 'Gleason's theorem' versus 'Rule for calculating probabilities in quantum physics', especially given other related rules.
4. Langauge differences. Proper names generally translate or carryover more efficiently than words.

Even if replacing Planck's name with Wien's had merit and Wien had precedence, arguments 1) and 2) apply.

 

[vanhees71]

I've never seen, how Wien derived his formula. Does somebody know the paper? The real breakthrough was of course Planck's discovery of the necessity of assuming that an electromagnetic wave mode of frequency $\omega$ can only exchange integer mutiples of energy quanta of the size $\hbar \omega$ with matter. I don't think that Wien had this idea before.

 

[fresh_42]

Wikipedia explains it very well:

"As expected, it [Wien's radiation law] has a radiation maximum, but delivers values that are too low for large wavelengths. [Rayleigh-James is correct for long wavelengths, but fails for short ones.] ... Max Planck corrected the above deficiencies in 1900 through a clever interpolation between Wien's radiation law (correct for small wavelengths) and Rayleigh-Jeans law (correct for large wavelengths) and developed from it Planck's law of radiation within a few weeks, which is also considered to be the birth of quantum physics."

Two false doesn't make one right, so Planck alone deserves the credit.

Edit: ... the more as he hated the idea of quantification!

 

[Demystifier]

Names for physical quantities or equations seldom reflect the person who actually first discovered them or used them correctly.

https://en.wikipedia.org/wiki/Stigler's_law_of_eponymy

 

[AVentura]

I've never seen, how Wien derived his formula. Does somebody know the paper? The real breakthrough was of course Planck's discovery of the necessity of assuming that an electromagnetic wave mode of frequency $\omega$ can only exchange integer mutiples of energy quanta of the size $\hbar \omega$ with matter. I don't think that Wien had this idea before.

I would be willing to believe this if one could show us how that gets you from Maxwell-Boltzmann to Bose-Einstein statistics, which appears to be the only change.

Wien does have a $h\nu = E$ substitution. I've heard that he deduced it from his observation that the peak frequency in his model changed linearly with energy, and he applied it to all frequencies.

And then there is the problem that Planck didn't seem to understand or accept that his paper violated classical physics. He was silent for decades as the world used his paper to say things he didn't believe.

 

[fresh_42]

I would be willing to believe this if one could show us how that gets you from Maxwell-Boltzmann to Bose-Einstein statistics, which appears to be the only change.

Evidence?

Wien does have a $h\nu = E$ substitution.

Evidence?

I've heard that he deduced it from his observation that the peak frequency in his model changed linearly with energy, and he applied it to all frequencies.

Evidence?

And then there is the problem that Planck didn't seem to understand...

Evidence?

... or accept that his paper violated classical physics.

Evidence?

He was silent for decades as the world used his paper to say things he didn't believe.

Evidence?

You claim a lot and tell us few. Instead you hide behind "It seems", "it appears", and "I have heard". Wikipedia has at least a list of references, all you have are unproven statements, supporting a physicist with questionable reputation.

 

[AVentura]

The change of statistics and the energy substitution within it are clear in the formulas.

There was a book that came out around 2000 regarding this all. People have written various articles about it. I read some of the articles. I'll try and find the name of the book.

I didn't know about Wien's reputation. Can you tell me more? But, I may someday tell someone that I've read or heard what you write.

Here's the book:
https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/

 

[vanhees71]

I've checked the original paper by Wien in the Annalen der Physik. He has derived his law from several ad hoc assumptions, which I cannot understand by reading the paper, and from the known Stefan's law that the total amound of energy radiated per time goes like $T^4$. I'd have to read several other papers, he's citing to fully understand all the assumptions going into his "derivation". There's no hint at quantization of energy exchange between the em. field and matter. I think Planck fully deserves the honor that $h$ (or nowadays $\hbar$) is named after him. Wien's paper is here:

http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1896_294_662-669.pdf

 

[AVentura]

I heard from some guy on some forum someplace that Wien expanded and contracted his cavity model adiabatically and noticed the shift in the peak predicted output, and that led him to $h\nu=E$. I'm not claiming it's true. I'm trying to find out.

 

[vanhees71]

Which paper by Wien are you referring to? In the paper I found through Wikipedia quoted above, there's no derivation using the cavity modes (which is of course standard nowadays).

 

[AVentura]

It's guess it's not true then. Then where did Wien get $h\nu=E$ from I wonder.

 

[vanhees71]

He just got his formula with a parameter which we today identify as Planck's constant (though he writes the spectral energy distribution in terms of wave length $\lambda=c/\nu$, i.e., in his paper nowhere the constant we call $h$ today occurs.

 

[AVentura]

I understand. He used a different representation for the expression.

btw, the German word for cavity, Hohlraum, is present in Wien's paper. Page 664, second paragraph.

Also:
https://www.nature.com/articles/162143c0

 

[fresh_42]

It's guess it's not true then. Then where did Wien get $h\nu=E$ from I wonder.

He did not. He had some constant and the wavelength.

 

[AVentura]

Which is equivalent.

 

[vanhees71]

I understand. He used a different representation for the expression.

btw, the German word for cavity, Hohlraum, is present in Wien's paper. Page 664, second paragraph.

Sure, there he refers to the well-known fact (since Kirchhoff's work on the problem) that in a cavity with boundaries at a constant temperature you get black-body radiation and that this also holds true for cavities surrounded by a gas separated from the cavity by transparent walls. What then follows is the derivation of the radiation spectrum emitted from a gas in thermal equilibrium following the Maxwell-Boltzmann equation. He then derives his radiation formula under the assumption of the scaling laws under changes of the temperature (p. 666). It's a pretty clever calculation, and Wien for sure deserved his Nobel prize for his work on black-body radiation (1911), but you really cannot say that he had any idea about the "quantum theory" of radiation as Planck relcutantly discovered and then has been worked out further by Einstein, leading finally to the development of quantum mechanics and (almost simultaneously) quantum electrodynamics, which of course is the today accepted foundation to derive the Planck radiation law from "first principles".

 

[fresh_42]

Which is equivalent.

But this doesn't imply anything. Any real number is proportional to $h$.

 

[AVentura]

Sure, there he refers to the well-known fact (since Kirchhoff's work on the problem) that in a cavity with boundaries at a constant temperature you get black-body radiation and that this also holds true for cavities surrounded by a gas separated from the cavity by transparent walls. What then follows is the derivation of the radiation spectrum emitted from a gas in thermal equilibrium following the Maxwell-Boltzmann equation. He then derives his radiation formula under the assumption of the scaling laws under changes of the temperature (p. 666). It's a pretty clever calculation, and Wien for sure deserved his Nobel prize for his work on black-body radiation (1911), but you really cannot say that he had any idea about the "quantum theory" of radiation as Planck relcutantly discovered and then has been worked out further by Einstein, leading finally to the development of quantum mechanics and (almost simultaneously) quantum electrodynamics, which of course is the today accepted foundation to derive the Planck radiation law from "first principles".

I don't think Wien had any idea about quantum theory. Can anyone explain how Planck got Bose-Einstein and how that's related to quantized energy? People, this was the only change he made in the formula. Wien must have known the value of the constant combined with the wavelength or frequency to make the spectral intensity peak fit experiment. Did Planck do anything different to find his value?

https://asmedigitalcollection.asme.org/HT/proceedings-abstract/HT2009/43567/59/356782
This paper probably has the answers.

Wilhelm Wien, working at Physikalisch-Technische Reichsanstalt in Charlottenburg, Berlin. He proposed a relation stating that the wavelength at which the maximum amount of radiation was emitted occurred when the product of the wavelength and the temperature was equal to a constant. This became known as Wien’s Displacement Law, which he deduced this by imagining an expanding and contracting cavity, filled with radiation. Later, he combined his Displacement Law with the T4 law to give a blackbody spectrum which was accurate over some ranges, but diverged in the far infrared. Max Planck, at the University of Berlin, built on Wien’s model but, as Planck himself stated, “the energy of radiation is distributed in a completely irregular manner among the individual partial vibrations...” This “irregular” or discrete treatment of the radiation became the basis for quantum mechanics and a revolution in physics

So Wien's cavity work was before his linked paper above. And Planck did notice something "irregular".

But,
https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/

As Kuhn points out, nowhere in his papers of 1900 and 1901 did Planck clearly write that the energy of a single oscillator can only attain discrete energies according to E = n epsilon= nhf, where n is an integer. If this is what he meant, why didn’t he say so? And if he realized that he had introduced energy quantization – a strange, non-classical concept – why did he remain silent for more than four years? Moreover, in his Lectures on the Theory of Thermal Radiation from 1906, Planck argued for a continuum theory that made no mention of discrete oscillator energy. If he had “seen the light” as early as 1900 – as he later claimed – what caused him to change his mind six years later? Could the answer be that he did not change his mind because he had not seen the light?

 

[AVentura]

I've tried to look into Wien's background for clues to the historical development. I did come across a claim that he was associated with nationalism. I think someone in this thread may be referring to this but doesn't want to elaborate. IIRC Planck defended his Jewish colleagues directly to Hitler. I suspect this is all related. For the record I would definitely prefer my hypothetical son to join Antifa over some fascist group, if I had to choose.

 

[PeterDonis]

a physicist with questionable reputation

I didn't know about Wien's reputation. Can you tell me more?

I've tried to look into Wien's background for clues to the historical development. I did come across a claim that he was associated with nationalism. I think someone in this thread may be referring to this but doesn't want to elaborate. IIRC Planck defended his Jewish colleagues directly to Hitler. I suspect this is all related. For the record I would definitely prefer my hypothetical son to join Antifa over some fascist group, if I had to choose.

All thread participants, please note that discussions about politics are off limits for this forum (and are even limited in General Discussion, since they can easily get out of hand). Historical questions about how a scientist arrived at a particular scientific equation, or whether such a derivation was scientifically correct, are ok, but please keep the discussion impersonal and free of political comments.

 

[vanhees71]

The big difference between Wien's and Planck's work is that Planck gave a derivation with a profound new idea, i.e., the discovery of quantization of the exchange of electromagnetic field energy with matter, $E_{\nu}=h \nu$, from any field mode of frequency $\nu$. He got to what we call Bose-Einstein distribution now by counting field modes in a cavity and using the quantized energy-exchange hypothesis, which was the only way to explain from the foundations of statistical physics (worked out by Maxwell, Boltzmann, and Gibbs) what he had found by a combination of phenomenological thermodynamics and interpolating between the Rayleigh-Jeans spectrum (known to be valid at low frequencies/long wave lengths) and Wien's formula (known to be valid at high frequencies/short wave lengths) to fit the high-precision data of his colleagues from the Technische Reichsanstalt (Rubens, Kurlbaum) who wanted to establish a standard for the upcoming lightning industry (particularly the then very new electric light). Wien's radiation law was a more or less luckily guessed semi-phenomenological formula.

 

[fresh_42]

For the sake of completeness, here is Planck's paper:
http://myweb.rz.uni-augsburg.de/~eckern/adp/history/historic-papers/1901_309_553-563.pdf

 

[AVentura]

Thanks. Looking for an English translation I came across this:
https://arxiv.org/pdf/physics/0402064.pdf
Pages 7 and 8 tell an interesting story, but I cannot reconcile it with what is in Planck's paper. But my German is very limited.

 

[vanhees71]

It's not a translation of Planck's paper. Here's a translation of the paper delivered to the German Physical Society (so to say the birth of the "old quantum theory" on Dec/14/1900):

http://hermes.ffn.ub.es/luisnavarro/nuevo_maletin/Planck (1900), Distribution Law.pdf

It's pretty similar to the Annalen paper linked in #24.

 

[AVentura]

I didn't realize Planck introduced Boltzmann's constant here. And essentially put the distribution that Wien used into the form we have today, with $E$. Okay, Wien wouldn't have known the energy of his states $E=\nu*constant$.