- #1
Nick89
- 555
- 0
Hi,
First of all, I hope this is the right forum for this. I was thinking about the brain teaser forum too, but thought this was more appropriate (at least, I think there's no trick involved).Someone on another forum asked the following question.
Suppose you have a wolf and a chicken on a cartesian x-y plane. The chicken starts running away from the wolf, but it moves only in the +y direction, with constant speed [itex]w[/itex]
The wolf, initially on the same axis as the chicken, separated by a distance [itex]d[/itex], will start to move toward the chicken, at constant speed [itex]v[/itex].
The crux is that the wolf always faces the chicken at all times. It does not 'think ahead' and try to intercept the chicken, he just empties his mind, stares at the chicken and starts running.Now, there's a few questions like 'how long does it take the wolf to capture the chicken', or at what distance did the wolf run, etc. But my question is, what is the path of the wolf??The setting again, as worded by the original poster:
First, the speed of the chicken is 0.5, and the wolf 0.7:
Relatively slow wolf
Then I increase the speed of the wolf to 1.5 and the interception is of course a bit sooner:
Relatively fast wolf
Here's two video's of these simulations:
I then derived an equation for the path, and graphed it, and got:
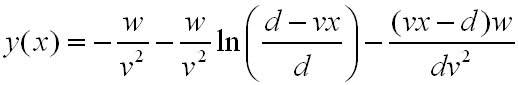
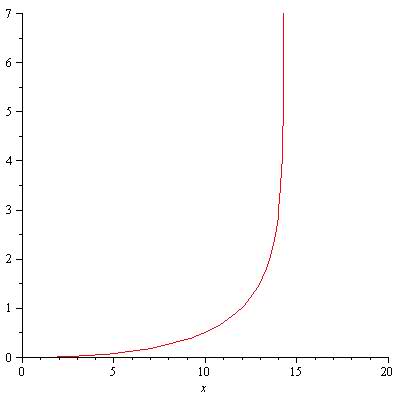
The derivation is as such:

This is based on the fact that the wolf faces the direction (d - vx, wt - vy) , which is the vector between the wolf and the chicken (since wt is the y-coordinate of the chicken). So the x coordinate of the wolf should increase in the (d-vx) direction, and the y coordinate in the (wt - vy) direction.
The graph above is for d = 10, v = 0.7 and w = 0.7 (as in the simulation).
The graph looks similar, but there's one major problem: the vertical asymptote is not at x = d!
I didn't think this was a problem at first, the wolf had merely captured the chicken already at x = d, and the graph is nonsensical after that.
However, I discovered that the position of the asymptote depends on the speeds v and w... For example, if the speeds are exactly the same, I would expect the asymptote to be at x = d (as always), and the wolf just trailing behind the chicken at a constant distance, never quite reaching x = d.
This is true in my graph if v = w = 1. It is NOT true if v = w = 1/2 or 2 or ... If v = w = 1/2, the asymptote is twice as far, at x = 20 instead of 10. If v = w = 2, it's at x = 5...
This is what I don't understand... I don't think my equation is correct therefor.
What do you think?
Also, I don't know any way to verify that the speed of the wolf is constant. It probably isn't at all, while it should be...
Anyway got any thought on this?
First of all, I hope this is the right forum for this. I was thinking about the brain teaser forum too, but thought this was more appropriate (at least, I think there's no trick involved).Someone on another forum asked the following question.
Suppose you have a wolf and a chicken on a cartesian x-y plane. The chicken starts running away from the wolf, but it moves only in the +y direction, with constant speed [itex]w[/itex]
The wolf, initially on the same axis as the chicken, separated by a distance [itex]d[/itex], will start to move toward the chicken, at constant speed [itex]v[/itex].
The crux is that the wolf always faces the chicken at all times. It does not 'think ahead' and try to intercept the chicken, he just empties his mind, stares at the chicken and starts running.Now, there's a few questions like 'how long does it take the wolf to capture the chicken', or at what distance did the wolf run, etc. But my question is, what is the path of the wolf??The setting again, as worded by the original poster:
We've been trying to solve this with a few people, and I think I have finally come close, except for one major detail.I wrote a quick and dirty simulation which shows the following behavior (blue = wolf, red = chicken):(1) There is a wolf and a chicken initially separated by some distance.
(2) The wolf runs at a speed that is faster than the chicken's.
(3) The chicken and wolf begin running at the same time. The chicken runs perpendicular to the line that would initially connect them and can only run in that direction. The wolf on the other hand runs such that he is always facing the chicken.
First, the speed of the chicken is 0.5, and the wolf 0.7:
Relatively slow wolf
Then I increase the speed of the wolf to 1.5 and the interception is of course a bit sooner:
Relatively fast wolf
Here's two video's of these simulations:
I then derived an equation for the path, and graphed it, and got:
The derivation is as such:
This is based on the fact that the wolf faces the direction (d - vx, wt - vy) , which is the vector between the wolf and the chicken (since wt is the y-coordinate of the chicken). So the x coordinate of the wolf should increase in the (d-vx) direction, and the y coordinate in the (wt - vy) direction.
The graph above is for d = 10, v = 0.7 and w = 0.7 (as in the simulation).
The graph looks similar, but there's one major problem: the vertical asymptote is not at x = d!
I didn't think this was a problem at first, the wolf had merely captured the chicken already at x = d, and the graph is nonsensical after that.
However, I discovered that the position of the asymptote depends on the speeds v and w... For example, if the speeds are exactly the same, I would expect the asymptote to be at x = d (as always), and the wolf just trailing behind the chicken at a constant distance, never quite reaching x = d.
This is true in my graph if v = w = 1. It is NOT true if v = w = 1/2 or 2 or ... If v = w = 1/2, the asymptote is twice as far, at x = 20 instead of 10. If v = w = 2, it's at x = 5...
This is what I don't understand... I don't think my equation is correct therefor.
What do you think?
Also, I don't know any way to verify that the speed of the wolf is constant. It probably isn't at all, while it should be...
Anyway got any thought on this?
Last edited by a moderator:
