Work by an ideal gas in a thermodynamic cycle

[merbear]

Homework Statement

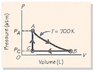
Two moles of an ideal gas are carried around the thermodynamic cycle shown in Fig. 18-29. The cycle consists of (1) an isothermal expansion A to B at a temperature of 700 K, with the pressure at A given by pA = 9 atm; (2) an isobaric compression B to C at PC = 4 atm; and (3) an isochoric pressure increase C A. What work is done by the gas per cycle? (See attached picture)

Homework Equations

pv=nRT

W=pdv

P=nRT/V

The Attempt at a Solution

W=nRT*ln(v2/v1)

For Pa:
9 atm= [2 mol*(.08205784 L*atm/k*mol)*700K]/V2

For Pb:

4 atm= [2 mol*(.08205784 L*atm/k*mol)*700K]/V1

V2/V1= 4/9

W=nRT(ln(4/9)) = 93.16 J (for A to B)

Here is where I got stuck. I can't seem to find the work for B to C without having variables in the answer. Once I can find the work from B to C I can add the work quantities to find the total (and ignore the value for C to B because the total work with no volume change is zero).

Any help in finding work from B to C would be appreciated.

Thank you

 

[anathema]

for your question. Based on the information provided, it seems that you have correctly calculated the work done in the isothermal expansion from A to B. To find the work done in the isobaric compression from B to C, you can use the equation W = PΔV, where P is the constant pressure and ΔV is the change in volume.

First, you need to find the change in volume, which can be calculated using the ideal gas law: V2 = nRT/P2. Plugging in the values given in the problem, we get V2 = (2 mol * 0.08205784 L*atm/K*mol * 700 K) / 4 atm = 287.403 L.

Next, you need to find the initial volume V1. Since the process is isochoric (constant volume) from C to A, we can use the same value for V1 as we did for V2, which is 287.403 L.

Now, we can calculate the work done in the compression from B to C: W = PΔV = (4 atm) * (287.403 L - 287.403 L) = 0 J.

Therefore, the total work done per cycle is the sum of the work done in the expansion from A to B (93.16 J) and the work done in the compression from B to C (0 J), which equals 93.16 J.

I hope this helps. Good luck with your calculations!

 

[Moetasim]

for your question.

I would approach this problem by first understanding the concepts involved in a thermodynamic cycle. A thermodynamic cycle is a series of processes that brings a system back to its original state. In this case, the ideal gas is taken through three processes: isothermal expansion, isobaric compression, and isochoric pressure increase. Each of these processes involves specific changes in temperature, pressure, and volume.

To find the work done by the gas in a thermodynamic cycle, we can use the first law of thermodynamics, which states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In this case, we can assume that the internal energy of the ideal gas remains constant throughout the cycle, as it is an ideal gas and there is no change in kinetic or potential energy.

Therefore, the work done by the gas in a thermodynamic cycle is equal to the heat added to the system. In this problem, we are given the temperature and pressure at points A and B, and we know that the process from A to B is isothermal. This means that the heat added to the system is equal to the product of the temperature and the change in entropy (Q = TΔS). Using the ideal gas law, we can calculate the entropy change for the isothermal process from A to B:

ΔS = nRln(V2/V1)

Substituting this into the equation for Q, we get:

Q = nRTln(V2/V1)

Since we know the values for n, R, T, and V2/V1, we can calculate the heat added to the system during the isothermal process.

Now, for the isobaric process from B to C, we are given the pressure at point C and we know that the volume remains constant. This means that the work done by the gas is equal to the change in pressure multiplied by the change in volume (W = PΔV). Since the volume remains constant, the work done by the gas in this process is zero.

Finally, for the isochoric process from C to A, we are given the pressure at point A and we know that the volume remains constant. This means that the work done by the gas is equal to the change in pressure multiplied by the change in volume (W = PΔV). Since the volume remains constant, the work done