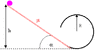
- #1
yoni162
- 16
- 0
Homework Statement
A ball is released from height h. The friction coefficient between the straight part and the ball is 'u'. I need to find the smallest h so that the ball doesn't fall off the track.
The angle alpha=45 degrees.
Homework Equations
Work of non-conservative forces = Change in mechanical energy
The Attempt at a Solution
I calculated the work done by the friction force while the ball is going down the straight part.
Wf=-u*mg*cos(alpha)*X
X=the length of the straight part.
We get that:
Wf=-u*mg*h
since cos(alpha)/sin(alpha)=1
Now I want to say that Wf=change in mechanical energy, so:
-u*mg*h=mg(0-h)+0.5*m(v^2-0)
when v=the velocity of the ball when it reaches the end of the straight part. We get:
v^2=g*h(1-u)
Now to the second part, the frictionless rail. Since all the forces are conservative now:
0.5*m*V1^2=0.5*m*V2^2+mg2R
When V1^2=g*h(1-u) -----> (the velocity we found before)
V2=the velocity at the top of the loop
So I want that V2>0, so after some work we get:
h>(2R)/(1-u)
but when I put in a numerical answer I'm told that I'm wrong. Is there a mistake in my solution?