Prove: (A - B)2 = A2 - 2AB + B2
The Greeks understood the totality of anything to always equal the sum of its parts.
We begin with the slightly easier task; a proof regarding (A + B) 2. (This proof was made by Euclid around 300 B.C.)
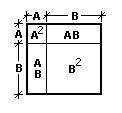
By inspection of the figure to the right, it is apparent (add the areas).
(A + B)2 = A2 + 2 AB + B2
But we need (A - B)². So Let's use the same square areas but assign new lengths for the previous A and B such that (A - B) arises as a factor. The second sketch, below right, shows these choices.
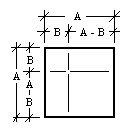
Again the area of the outer square will equal the sum of its areas interior:
A2 = (A - B)2 + 2(A - B)B + B2
A2 = (A - B)2 + 2AB - 2B2 + B2
Now, rearrange and collect the above equation to obtain:
(A - B)2 = A2 - 2AB + B2 Q.E.D.
A technique used in geometry is also used in thermodynamics. Break things apart, solve, then put the pieces back together.
Prove: (A - B) 2 = A 2 - 2AB + B 2
The Greeks understood the totality of anything to equal the sum of its parts.
An easy way to precede is to begin by with a slightly easier
task regarding ( A + B )². The common result was first obtained by Euclid around 300 B.C.
Premise presently unwritten!