THERMO Spoken Here! ~ J. Pohl ©
     TOC NEXT    ~   10

Vector Proof of Trigonometry Laws

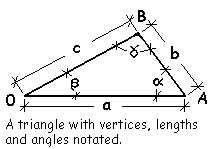
A typical planar triangle is shown below. The triangle vertices, lengths of sides, and angles are identified by notation. Trig Laws 1

We choose to define a vector space to be the plane of the triangle. We name the two-dimensional space 0XY. We place the origin of the space at the A0B vertice of the triangle and we align its X-axis along the triangle side, 0A. The Y-axis passes through the origin, orthogonal to the X-axis. To be completely defined a vector space must have a unit vector basis. We choose the uppercase letters, I and J, to represent unit vector directions for the X and Y coordinates, respectively.

The second image (right) shows the planar triangle with a our vector space imposed upon it. Vectors are easy to use and very productive in understanding. Read this example slowly and thoroughly. Return to your algebra or trig book and compare these TRIG LAW proofs with those.
v

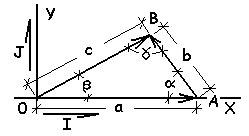
Next we state something we believe to be so completely true that you and I can accept its truth axiomatically. (The simplest axiomatic truth is: "We exist." The proof goes: "I exist." No argument about that. I see you and you say, "I exist." Conclusion: "We exist." It is an axiomatic truth that we exist.

So for this triangle it is axiomatically true for the vectors of its sides:

0A + AB = 0B

(As an aside, note that 0A + 0B = AB is false, that is, axiomatically wrong).

The sketch below shows how these vectors are written in component form.

v

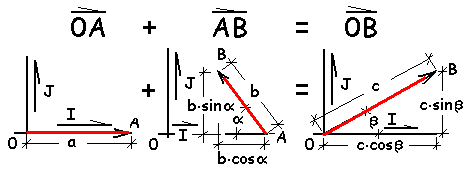
From the figures we see:

a I - b cosα I + b sinα J = c cosβ I + c sinβ J

Equivalently,

(a - b cosα) I + b sinα J = c cosβ I + c sinβ J

From the J component we have, b sinα = c sinβ which divided by bc yields:

Law of Sines:    (sinα)/c = (sinβ)/b

Next we take the I component relation; ( a - b cosα) = ( c cos β) and square it to obtain (i):

(i)  a2 - 2 a b (cosα) + b2 (cosα)2 = ( c cosβ)2

The J component relation is (b sinα)2= (c sinβ)2. We square this expression also to obtain:

(ii)  (b sinα)2= (c sinβ)2

Next expression (i) and (ii) are added:

[a2 - 2 a b (cosα) + b2 (cosα)2] + (b sinα)2 = c2(cos2β) + sin2β)

The component relations,   J are relations, square each of them and add their squares:

I:    ( a - b cosα)2 = ( c cosβ)2    and     J:   (b sinα)2= (c sinβ)2

a2 - 2 a b (cosα) + b2 (cosα)2 = c2 (sinβ)2

b2 (sinα)2 = c2 (sinβ)2.

With a bit of algebra we have:

Law of Cosines:    a2 - 2 a b (cosα) + b2 = c2