Manometer and Bourdon Gage
The elevation of the horizontal pipe is slightly above sea level. Water flows through a pipe that has been fitted with a manometer and a Bourdon gage. Use the readings of the manometer and Bourdon gage:
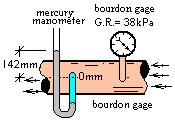
Calculate the pressure of water flowing through the pipe.
♦ We always start at a place in space where the pressure of the fluid is known.
Manometer At the center-line of the pipe but outside in the air about it; the pressure there is atmospheric pressure. Let that point be our first (known) pressure. The path now moves upward 142mm to the upper surface of the mercury. From there follow a hydrostatic path through the mercury (gage) to the center-line of the flow of water.
patm + 13,600 kg/m39.81 m/s2(0.284 m) -1,000 kg/m³9.81 m/s2(0.142 m) = 137.8 kPa
Bourdon Gage: This gage is connected to the side of the pipe at its center-line. Thus atmospheric pressure plus the gage reading (G.R.) will equal the pressure of the water inside the pipe.
patm + G.R. = pwater or 101.3 kPa + 38 kPa = 139 kPa
One pascal of pressure difference is very small. The Bourdon gage might be incorrect - it had to be calibrated. The water pressure should decrease in the direction of flow.
Manometer, Bourdon Gage

The elevation of the horizontal pipe is slightly above sea level. Water flows through a pipe that has been fitted with a manometer and a Bourdon gage. Use the readings of the manometer and Bourdon gage:
Calculate the pressure of water flowing through the pipe.
Premise presently unwritted!