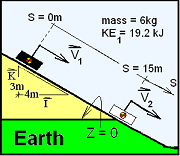
Planet Gizmo
On Planet Gizmo a small block was observed, State (1), sliding down an inclined plane. A "down-the-plane" coordinate, "s", was imagined with the block at its origin, s = 0 at the time, t = 0+. The mass of the block is: m = 8kg. Initially the elevation of the block and its its kinetic energy were: zB,1 = 6m and KEB,1 = 4J, respectively.
A datum for vector space and potential energy (x = 0, z = 0) and a unit vector basis (I and K) are defined on the sketch.
| Position: | PB,1 = | PB,2 = |
|---|---|---|
| Speed: | |V|B,1 = | |V|B,2 = |
| Velocity: | VB,1 = | VB,2 = |
| Local Acceleration (on GIZMO) |
gGIZMO = | Note: These characteristics and properties can calculated but not in the order listed. Place answers in these boxes. |
| Momentum: | mVB,1 = | mVB,2 = |
| Potential Energy: | PEB,1 = | PEB,2 = |
| Kinetic Energy: | KEB,1 = | KEPB,2 = |
Later at State (2), the time is t = 4 seconds and the occurs later Later, at time
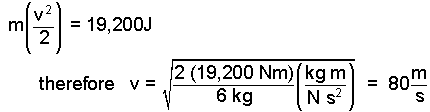
Write the Velocity as speed times direction.
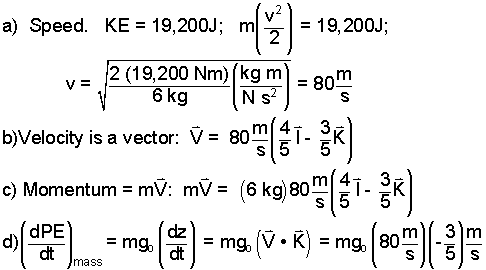
Write its Momentum in component form.
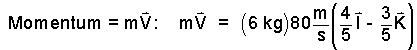
Planet Gizmo
Consider a block of mass 6 kilograms. The block was first observed moving down a frictionless plane with a kinetic energy of 19,200 Joules, State (1). We set the time (the moment of first observation) to be, t = 0+. The coordinate "S," is added to denote distance down the plane.
Calculate the speed, velocity, kinetic energy, position as a function of time, potential energy, and position and velocity in 3 seconds (not necessarily in order):
Premise presently unwritted!