Rock Falls onto a Spring
State (1) shows a rock of mass, m, supported by a cord above an upright spring. There is "touching" contact but the initial spring force is zero.
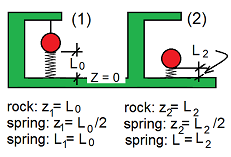The length of the spring is its upright free length, Lo. Upon cut of the cord, the rock falls and compresses the spring to its shortest length, whereupon the spring pushes the rock upward and so oscillating, eventually both come to rest - State (2).
Calculate:
(i) The spring constant needed such that the shortest spring length is Lo/2.
(ii) The increase of temperature of the spring once motion ceases.
♦ Shortest Spring Length: The event of the spring involves forces relevant to the mass. We begin with Newton's 2nd Law written with the mass as system. The spring force, Fs acts upward and the gravity force, Fg,rock, acts downward. A technique with the 2nd Law equation is to multiply it by dzK. The equation setup is:
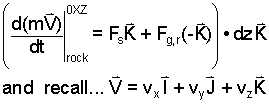
The momentum of the rock is scalar multiplied by the unit vector, K.
Below the scalar multiplication is done. Right of equality the spring force and gravity forces are expressed. Left of equality the momentum of the rock is rearranged.
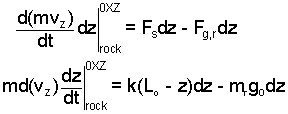
Spring constant times compression and gravity force are specified.
Rearrangement of momentum (left-of-equality) proceeds by steps... i) original term, ii) after chain rule differentiation, mass being constant, iii) a rule of differential calculus permits the "moving" of differentials horizontally in the denominator, and iv) identify dz/dt as vz.
These steps are details
of understanding.
The event "Shortest Spring Length" commences upon cord cut and ends at the shortest length. Physically this means the velocity initially and finally velocity equal zero.
Momentum zero (initially and finally)
means sum of forces is zero!
Now carefully integrate Eqn-4 and sort out the algebra.
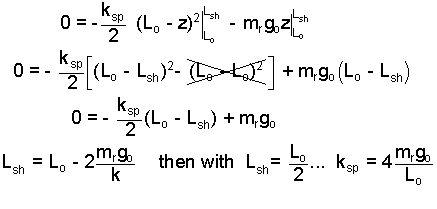
This is the step-by-step integration
and algebra. Please check this!
Thus we have an equation for the spring constant we need.
♦ Increase of Temperature: By Newton's 2nd Law the final elevation of the rock can be determined:
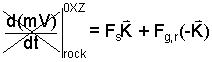
Not moving means constant-zero, momentum
and the sum of forces is zero!
A consequence of mechanical equilibrium.
Take the system to be the rock and spring. For the event no forces "at the boundary" are displaced, hence work equals zero. Also since the event happens promptly, heat is assumed to be negligible. Thus the energy equation is:
Boundary forces are not displaced.
Too quick for heat.
Both the rock and the spring experience changes of potential energy. In addition the spring, upon compression, will experience a change of internal energy. The energy increments of the event are:
Energy change is the sum of three increments.
Potential energy change with elevation change is understood. Take the datum for the rock "at its bottom" (where it contacts the spring). For potential energy of the spring we use its "center of mass" assumed located at "mid-length."
Potential energy changes are accounted.
Model the spring as being a simple, "linearly-elastic" material. Then its internal energy will be a function of temperature (T) and length of compression (Lo - L). For the event, the spring length will be less than the free length, Lo.
Every substance has temperature as a property!
The differential, dU, has two parts; one thermal, the other mechanical.
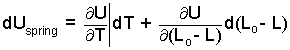
The internal energy gets greater as the spring gets shorter.
The coefficient for "dT" is the specific heat. The coefficient for "d(Lo - L) length is the linear spring force. Enter these:
Differential internal energy
of a linear spring.
Integration of Eqn-8 yields Eqn-9, our expression for ΔU.
Increment of internal energy of a linear spring.
Returning to Eqn-5, with ΔUspr, our equation becomes:
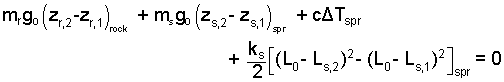
Energy Equation ~ increment form.
By the figure of the event, we can identify the Δ z's and the Δ L's.
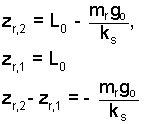
Properties for the rock.
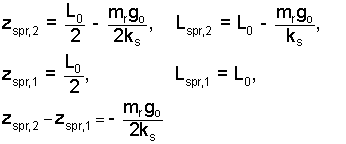
Properties for the spring.
Now use the information of Eqn-12a and 12b. Enter the proper "differences" into Eqn-10.
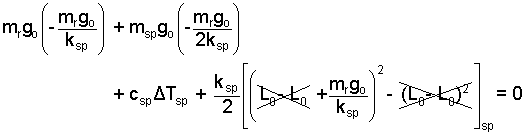
Energy increments made specific.
Collect the terms. See what things look like.
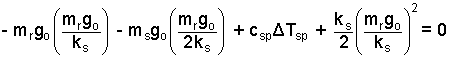
Can you "condense" this?
Some might say the mass of the spring is "small."
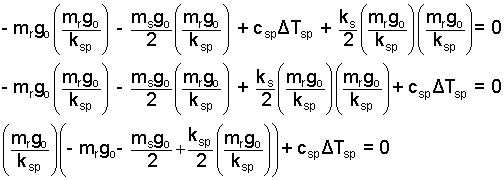
Algebra is the hardest part of physics.
We applied steadfast principles of physics. I'm going on vacation with my wife next week. I'll take this along and straighten out the algebra!
Rock Dropped on a Spring
State (1) shows a rock of mass, m, supported by a cord above an upright spring. There is "touching" contact but the initial spring force is zero. The length of the spring is its upright free length, Lo. Upon cut of the cord, the rock falls and compresses the spring to its shortest length, whereupon the spring push the rock upward, and so, oscillating and eventually come to rest - State (2).
Premise presently unwritted!