Karnaugh Maps: An Essential Tool for Understanding Complex Digital Logic Designs

[Kenneth Mann]

In the next few insertions, I shall attempt to explain the concept and operation of Karnaugh Maps. I hope this will be of interest to someone. I would welcome your questions and opinions.

Initial Concept

M. Karnaugh published a paper in October 1953, in which he described the basic principles of what has since become known as the ‘Karnaugh Mapping’ technique. In this re-examination of that technique, attempt will be made to explain, as thoroughly as possible, the ideas behind this technology, and to show some ways in which it can be used to simplify the digital logic design function, and to demonstrate some of the exceptional power and flexibility that can be exercised in this graphical mapping method. Hopefully, when finished, this tutorial will provide a basis for facilitating much of the process of designing many of the essential components that are used in digital assemblies.

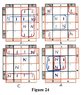
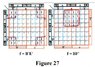
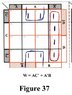
As a start, three attachments are included with this insertion in the string; a set of four-variable K-Maps, a set of six-variable K-Maps, and a 'Truth Table' framework that can be used with maps of up to eight-variables. These can be printed and used whenever needed. In this tutorial, we will show how these are used together. An eight-variable map, and possibly a ten-variable map will be included later.

First, we shall explain the reasoning behind the map, then we shall illustrate its use.

Concept Refinement

The Karnaugh map, as it was initially envisioned, was considered to be directly capable of minimizing Boolean equations of up to only four variables. To handle a greater number of variables, two or more maps had to be used together, a somewhat cumbersome process - - - and this still entailed a practical working limit of up to approximately six variables. (The process essentially extends the map into three dimensions.)

Then, about a decade after Karnaugh's paper, an individual named Matthew Mahoney observed a symmetrical reflecting approach behind the process of map construction which showed that maps could be extended in design beyond four variables, and from that approach he came up with a slightly different design which, was termed the 'Mahoney Map'. That approach will be shown (in passing) in a future insertion.

KM

 

[Kenneth Mann]

The basic Map Structure

1.) The basic Map Structure

The Karnaugh Map is made up essentially of an array of adjacent rectangular "cells", each of which represents a predefined logical state (off or on; "0" or "1") of the total set of possible variable value combinations represent-able, thus if the map is designed for three variables (for example), then it would have 2^3 (or 8) cells. We will demonstrate how the cells are arranged within the map.

First, however let it be stated that the K-Map is simply a vehicle for graphically performing and demonstrating the application of the various Boolean axioms (which are given in table 1). As an example, figure 1 shows a couple of simple two-cell maps (the smallest possible size K-Map). A map of this size can represent only one variable (not very useful in a practical application, but useful for demonstration). In the first of these two maps, we state that the value "A" exists in its asserted state. As such, there is nothing more that we can say about it. What we get out is exactly what we put in - - - in exactly the same form. It cannot be refined any further

In the second map of figure 2 however, we state that both "A" and "A' " are present, and we put both into the map. In this case, we know from the axioms of table 1 (Boolean Postulates and Theorems) that A + A' = 1, the Postulate 5 case, so that the need for the "A" variable disappears (it is absorbed into the "1"). As result, no logic devices or enabling signals would be needed for this case, because the 'output' is always present. ("1" means all the time.)

The solution of the K-Map generally works out in this way (mostly via application of Postulate 5). This is the most prevalent postulate operable in K-Maps, but not the only one. With it, for each two terms of the map that have all variables alike except for one, that pair of terms has an N + N' grouping, and thus the "N" variable drops out of that term. The task then is to arrange the cells within our map so that each symmetrical cell-group pair - - - can have one and only one variable that changes (this we will explain more completely later)

An even more useful pair of examples are given in figure 2. In 2a) we mark in the values to represent (A'B + AB' ) (represented by ones in the map). Examination of that map shows that there is no symmetry across the axis between the B' and B Rows - - - - or, across the axis between the A' and A Columns. Because of this, neither a variable in "A", nor a variable in "B" will drop out (be reduced).

On the other hand, (in figure 2b), where we initially defined the values (AB' + AB), there is a symmetry across the axis between the B' and the B rows, so that in this case, the B-variable will drop out (Postulate 5), leaving "A" as the minimized value.

The important factor in the design of the Karnaugh map is the fact that the map is laid out so that, across any "axis" one and only one bit in the binary value of the term(s) represented within, may change. This means that one and only variable can change (from N to N' or vice versa) across that axis.

KM

 

[Kenneth Mann]

2) Map Layout Choice

2) Map Layout Choice

Before discussing the actual operation of the Karnaugh Map, a few words are in order concerning the choice of directions for laying the map out. The first of these possible choices would be the use of a column-ordered map such as that shown in figure 3. In this arrangement, the lower-ordered variables (A, B, etc.) are arranged into the columns, with their characters placed vertically along the left (and maybe the right) of the map. The higher-ordered variables (such as D, E, etc.) are arranged into the rows, and are depicted horizontally across the top (and maybe the bottom) of the map.

The second arrangement is into a row-ordered map like that of figure 4. In this arrangement, the lower-ordered variables (A, B, etc) are arranged into the rows, with their defining characters represented horizontally across the top (and maybe the bottom) of the map. The higher ordered variables (such as D, E, etc.) are arranged into the columns and their defining characters represented vertically along the left (and maybe the right) of the map.

Many people use the column-ordered representation, possibly because that is the way Karnaugh laid his out. I prefer the row-ordered map, because that is the orientation I find most familiar in everyday life. This is the way we were taught from elementary school to orient almost everything. In reality, it probably makes little difference. The maps will usually be filled in, by-the-numbers, directly from truth tables, with little concern for orientation (we will demonstrate that later). Only when reading the maps will the layout usually come into play to any noticeable degree, and then the variables will be clearly delineated if the accompanying map forms are used.

KM

 

[Kenneth Mann]

K-Map Numbering Method - Part 1

K-Map Numbering Method - Part 1

The position at which each possible minterm* is located within the K-Map corresponds directly to the number which is assigned to that cell in the map, thus the location of each cell of the map must be selected so as to assure that the following is true: - - - From any cell within the map, to its adjacent (vertically or horizontally) neighbor cell - - -one and only one bit in the cell numbering may change. This numbering sequence is accomplished as follows.

Referring to figures 5 and 6, we build a Karnaugh Map in the following manner: First we start with a base, or root, cell. To this cell we assign the number "0". From here on, we add cells and assign their cell numbers by what may be likened to an 'unfolding' process. This process we can liken to that of continually producing a new group of cells exactly like the ones we already have, but positioned exactly on top of the one(s) we already have. Each cell of this new layer, then has the same value as the one directly beneath it, plus 2^M (where M is the number of the 'unfolding' operation, starting at "0"). Each 'unfolding' step, is then done from the boundary (axis) following the last presently existing cell in the map (horizontally or vertically).

For a row-ordered K-Map, we first generate the cells of the first row as is illustrated in figure 5. The number of 'unfolding' operations will depend upon how wide to make the map. (In the illustration, we perform three 'unfolding' operations, in order to produce an eight-cell-wide map.) Starting with the "zero" cell, we generate a new cell on top of it, and give it the value "1" (0 + 2^0 = 1). Then we unfold this out - - around the 'axis' (figure 5.b) following the "0" value cell, and now have a two-cell-wide map. Next, we repeat the process, generating two new cells atop the ones we have, and give these new cells the values (0 + 2^1 = 2) and (1 + 2^1 = 3). Then when we unfold these out (figure 5.c), we have the map cells "0", "1", "3" and "2". Finally, when we perform the process again (this time adding 2^2), we end up with the cells "0", "1", "3", "2", "6", "7", "5" and "4" (figure 5.d).

We then produce the remaining rows of our K-Map in the same manner, but by unfolding each new row around an axis beneath the row from which it is derived (figure 6). For example, row 2 is formed by generating it above row one, with each cell in row 2 having the same value as as the cell beneath it, plus 2^3 (figure 6.b). The same process is then repeated to generate the next pair of rows (figure 6.c)

What we now have, is a map like that of figure 7. If we trace adjacent cells through the map, we now get a number arrangement which looks essentially like that of the standard 'Reflecting Gray Code" numbering sequence. In this sequence, every sequential number has one and only one bit different from its sequential neighbor (predecessor or following number). To be sure, our map doesn't necessarily come from the standard reflecting gray-code sequence, but is simply dirived in much the same way, thus we end up with the same pattern.

What's more, all the cells of the map are arranged so that each has only a one-bit difference from its neighbor, vertically or horizontally (the vertical relationship, other than at the dnds of rows, would be of no concern with gray-codes). The way the map was generated assures this two-way relationship.


KM

[* If there are N binary variables, then there will be a total of 2^N possible Simple-Sum-of-Products (SSOP)combinations of these N-variables, where each of these 'terms' contains each variable, represented in either its normal or its complemented (not) form. Each or these 2^N possible terms is called a minterm. For example, if there are two variables A and B, then there are four possible minterms; A'B', AB', AB and A'B.]

 

[Kenneth Mann]

4. Karnaugh Map Numbering Method - - Part 2

4. Karnaugh Map Numbering Method - - Part 2

In figure 8, we have a binary representation of the cell numbering of the K-Map, A straight examination shows us that every cell within the map has a binary number value in it which is identical to that of each of its adjacent cells (above, below and to both sides), except for one bit (a different bit in each direction). One bit, when going from any cell to a neighbor is all that changes. Furthermore, going from any cell to one neighbor, the bit that changes is different from the bit that changes if going to another neighbor from that cell. Finally, we can see a pattern that occurrs along any row or column of cells, when going to the next adjacent row or column. The bit that changes, is the same for all cells along that row or column. In other words, across every "axis" between rows or columns, there is a particular bit that changes. The significance of this is the fact that, along any axis, there is a N-N' variable pair combination, which is the only variable that changes when crossing that axis - - - thus every cell pair across that axis allows the elimination of that particular variable.

The reason for this can be seen from the way that the cells and groups of cells were "unfolded", to create our numbered cell groups, both horizontally and then vertically. This created the distinct axes, each of which is identified by - - - the bit that changes as that axis is crossed when going to adjacent cells. [What is not yet readily apparent, is the fact that (for maps of more than four variables) a one-bit change occurs not only for adjacent cell rows/columns, but also for all that are symmetrically located across each of these axes. This we shall discuss later.]

If we thus examine figure 9, we see (in the example of a four-variable case) which bit changes as each axis is crossed. For numerical convenience, "A" represents the rightmost bit, "B" the next to rightmost bit, and so on. Finally, figure 10 depicts several possible configurations of K-Maps, set up and numbered according to the rules which we have established. By substituting the binary values for each of the cell number values (shown in decimal) we can readily verify the bit-changes across each axis.

There is more to come - - - KM

 

[Kenneth Mann]

5. The Mahoney Map

5. The Mahoney Map​

In the early 1960s, Matthew Mahoney more precisely defined the basic mechanism through which the logic-map operates. Using this principle (which we have already laid out) he defined and laid out what came to be called the "Mahoney-Map". Essentially, the Mahoney Map is a variation of the Karnaugh Map, and the principles will apply equally in both cases.

Two examples explaining the workings of the Mahoney Map are shown in figures 11 and 12. The basic difference of the Mahoney Map from the Karnaugh Map is the fact that, where the K-Map can be laid out in either a "column-ordered" or a "row-ordered" manner (as we described in insertion number 2), the M-Map is laid-out in an alternating Row-Column manner - - - and can be numbered using a series of repeatingly reversing "Z" patterns. Explanation of the Mahoney Map is as follows:

The same reason that underlies Karnaugh Maps also applies to Mahoney Maps. This is illustrated in figure 11. There (in figure 11-a) we start out with one cell ("0") and expand from there by symbolically rotating that cell about the axis to the right, and adding "1" (2^0) to the original value (0), and putting the sum (0 + 1 = 1) into the new cell. Next we rotate two cells we now have downward, and add "2" (2^1) to each of the newly created cell values (0 + 2 = 2) and (1 + 2) = 3. Next (in figure 11-b), we rotate what we now have, to the right, and add "4" to each cell value to get (0 + 4 = 4), (1 + 4 = 5), (2 + 4 = 6) and (3 + 4 = 7). Then we rotate our new 8-cell group downward (again), and this time add "8" to each and get, values 8 through 15 (also in figure 11-b). Next (in figure 11-c), we rotate our cells right again, and add 16 to each. Finally here, (in figure 11-d), we rotate our cells downward again, and add 32 to each. This process, we can see, accomplishes the same thing as with the Karnaugh Map, except with alternating rotations to the right and then down.

There was also a method defined for drawing the M-Map, which is easy to remember. This consists of drawing in consecutive numbers starting at "0", and going through continually repeating and reversing "Z" patterns (as shown in figure 12). Observing figure 12-a, we see how the numbering of M-Map cells means putting in the consecutive numbers in reversing "Z" patterns. Cells "0" through "3" form a standard "Z", numbers 4 through 7 go in with a reverse "Z" pattern, numbers 8 through 11 go in with an inverted "Z" pattern, and numbers 12 through 15 go in with a reverse-inverted "Z" pattern. Also, as shown in figure 12-b, Those four, four bit entries also form a (larger) "Z" pattern. There are four of these larger "Z" patterns, which each also derive from four of the smaller patterns. The second of these larger patterns is also reversed, the third is inverted, and the fourth is reversed and inverted. Then finally, the four larger Z-patterns are themselves put in in a Z-pattern. Basically the K-Map and the M-Map configurations offer the same capabilities, and are used in the same manner. Comparative advantages of the two types are as follows:

Mahoney Map Advantages:
A) This map is easier to draw-up, especially in the larger sizes. It is necessary only to put in sequential decimal values into a set of continually reversing "Z" patterns. The actual (reflecting gray-code-like) sequence that is being generated is hidden in the mechanics of the construction process.

B) Maps of different sizes always have the same cell-numbers all located in the same places.

Karnaugh Map Advantages:
A) This map is more familiar to more people, and thus more communicatable.

B) The Variables in this mapping arrangement remain in order, rather than alternating - - making them somewhat easier to follow.

Discussion from here on, will be limited to the case of the Karnaugh Map.

KM

 

[Kenneth Mann]

7. Karnaugh Map Annotation Choices

7. Karnaugh Map Annotation Choices​

In passing, we look at the various methods used for annotating the Karnaugh Map, not attempting to suggest or endorse any, but to indicate some things that have been used, and that might be used at various times in this string (sometimes because of the constraints imposed by the software being used here (MS Word, etc.).

First, brief mention is made of the ways used to indicate occurrence of a minterm* within the map. Figure 15 shows some of these. The top view, illustrates use of the value "1", indicating "presence" or "yes". This is the most commonly used indicator, though other marks, such as "X"or several other characters have also been used. The last entry, the "slash" was recommended by Mahoney for his map configuration. In this series of string insertions, the "1" shall be used (at least in most cases).

Figure 16 shows ways of grouping the cells (minterms) for minimization purposes. (The bottom style was recommended and used by Mahoney.) It should be noted that none is absolutely ideal in the case of complex maps of greater than four variables, because of the need which sometimes arises in those cases, to link non-adjacent cells.

* See insertion number 3.

Will try to get #6 Tomorrow, after some drawing erors are corrected. - - - KM.

 

[Kenneth Mann]

6. Closed Map Structure

6. Closed Map Structure​

The one point to be emphasized in this insertion, is the fact that the Karnaugh Map is a closed entity - - - thus it has no outside boundaries. Karnaugh himself described it as being like a torus, such as that shown in figure 14 (in this case, a six-variable map is shown).

Figure 13 is of a four-variable map showing the relationships across what appear to be the outside boundary axes (but since the map is 'closed' these axes are not outside boundaries). The first assertion we make here, is that the (so called) top axis of the K-Map, and the (so-called) bottom axis are not two separate axes, but are the same axis, coming, in this case, between the C'D row and the C'D' row. Arrows show the transition across this axis, Just as is the case across all other axes, one bit value in the representation changes (in this case, the "D" bit representation). Similarly, there is only one vertical axis between the A'B and the A'B' columns, and it is characterized in the same way, verifying that this is a completely closed structure.

KM

 

[Kenneth Mann]

8. The Karnaugh Map is An SSOP Tool

8. The Karnaugh Map is An SSOP Tool​

The Karnaugh Map was designed to take a known sum (OR'ing) of conditions, each of which is given as a minterm of the variable set (for example, A, B, etc.) being evaluated - - - which is a SSOP (Simple Sum of Products) function - - - and to minimize this function, in order to produce another SSOP function which will use the fewest number of gates.

To illustrate what is meant here, we can refer to the example in figure 17, in which we have the four variables (A, B, C, D). We are initially given the conditions; which in this case, consist of Eight minterms (of a possible sixteen). This can be expressed as the SSOP function:

f = A'B'C'D' + AB'C'D' + A'BC'D' + A'B'CD' + AB'CD' + A'BCD' + A'B'CD + AB'CD

This function is solved in the K-Map, by assigning each of the minterms to its respective cell - - - to derive the minimized version of the function:

f = A'D' + B'C + B'D'

- - which is also a SSOP form. Finally, shown in figure 17, are two gate combinations that can be employed to generate this function. (a NAND - NAND pairing is equivalent to AND - OR.)

NOTE: It can also be pointed out here, that whereas the K-Map is designed to readily work with SSOP functions, it can with a little manipulation, also yield SPOS (Simple Product of Sums) results, such as that of figure 18. (P.S: Here instead of AND - OR, we could have used NOR - NOR)

Next: The dynamics of minimization. - - - KM

 

[Kenneth Mann]

9. Dynamics of The Minimization Process

9. Dynamics of The Minimization Process​

The example shown here is not a practical application, nor is the method of solving the example the usual approach (there are too many minute steps taken), however it is intended to illustrate what takes place inside the map minimiation process.

In this case, we select every cell within the map to be 'marked'; in other words, all the minterms are present. This is shown in figure 19-a, in which every cell has a "1". We have additionally illustrated the values of the minterms represented within each cell.

In figure 19-a, we can see that each cell in the first column has a value identical to its adjacent neighbor in the second column, except for the value of the "A" variable. As an example, the values in cells "0" and "1" are A'B'C'D' and AB'C'D' respectively, thus when we observe these two cells grouped together (OR'ed) we get:
A'B'C'D' + AB'C'D' = B'C'D'(A' + A)
= B'C'D' (1)
= B'C'D' - - - - thus, we have eliminated the "A", and get cells "0" and "1" to contain what is in figure 19-b.
The same is the case for the remaining cell pairs between columns "1" and "2", and also those between columns "3" and "4". What we get then is that shown in figure 19-b.

In like manner, in figure 19-b, each cell-pair in combined columns "1" and "2" , has values that are the same as those in combined columns "3" and "4", except for the value of the "B" variable, thus if we combine (for example) the values of cells "0/1" and the values of cells "2/3" (by OR'ing them), we get
B'C'D' + BC'D' = C'D'(B' + B) = C'D'
- - - thus we have now eliminated the "B" - - - in the first row - - - and can do likewise for the other three rows.

What we have left, is the groupings shown in "C". Now we notice that the valus of the term in row "1" is the same as that in row "2", except for "C", and we thus have:
C'D' + CD' = D'(C' + C) = D'(1) = D'
The same is the case between rows "3" and "4", and we thus have:
C'D + CD = D(C' + C) = D

Finally, in figure 19-d, - - - if we combine (by OR'ing) the two remaining cell groupings, we get:
D' + D = 1
This simply implies that the "output signal" is "1" meaning that it is always present - - - and requires no logic to enable it.

This example, in a practical sense, is basically useless in the "real world", but it is also informative. It shows what takes place during the map minimization process.

KM

 

[Kenneth Mann]

10. A Few Simple Rules

10. A Few Simple Rules​

Now we are ready to jump into the map minimization process in earnest, but before doing so there are a few rules that should prove helpful. Most of these rules concern the process for gathering the minterms ((marked cells) together into groups, and do not concern the form used to delineate these groups. (In this series, choice is made to "circle" the selected groups of cells.

Map Cell Entry Rules:
Rule 1: Each minterm (term containing all variables, in either the asserted or the negated state) going into a map will occupy one (and only one) cell.
Rule 2: If a term has fewer than the maximum variables, expand it to form minterms, by adding all missing variables. Do this by inserting in place of the original term, two new terms, one with the added variable in its negated state and one with the added variable in its asserted state. If one variable is thus added, two new terms will be formed; if two are added, four new terms are formed; if three are added, eight new terms are formed; etc.

Map Grouping Rules (Cell Grouping):
Rule 3: Maps have no "boundaries". They are closed.
Rule 4: Each cell grouping (circling, etc.) must contain exactly 2^N cells, where N = 1, 2, 3, etc.
Rule 5: If 2 cells are grouped, one variable will be eliminated.
Rule 6: If 4 cells are grouped, two variables will be eliminated.
Rule 7: If 8 cells are grouped, three variables will be eliminated.
Rule 8: If 16 cells are grouped, four variables will be eliminated.
Rule 9: Any valid group of cells must be rectangular (and in a map of four or fewer variables, they must be contiguous).
Rule 10: Any Cell grouping must be symmetrical across each of its dividing axes.
Rule 11: Make each cell grouping being formed, as large as possible.
Rule 12: The overlapping of cell groups is perfectly acceptable.
Rule 13: Leave no marked cell behind(when finishing with groupings).
Rule 14: Include no unmarked cells within a grouping (except possibly "don't care" cells).
Rule 15: Avoid including "redundant" groupings.

Hints:
Rule 16: There may be multiple solutions that are correct.
Rule 17: Any correct answer will include the the smallest number of terms, and the lowest variable-per-term count, and will include all of the available minterms.

Map Solving Rules: Finally, when reading out the term value for grouping that has been constructed (circled, etc.) on the map, there are these additional rules.
Rule 18: There must be a product term (in the SSOP solution) for each grouping that has been formed.
Rule 19: If a grouping intersects a variable (N) in both, its negated and its asserted states (N' and N), drop that variable from the term being formed.
Rule 20: If a grouping intersects a variable (N) in only its negated state (N') include it in the term in its negated state. Likewise, if the grouping intersects that variable in only its asserted state, include it in its asserted state.
Rule 21: Check to verify that rules 5 through 8 have been complied with.

We are now ready to start!

KM

P.S. Some additional Truth Tables are also included to make it easier to work with eight variable Karnaugh Maps. One of these will be submitted soon.

 

[Kenneth Mann]

11. Filling and Grouping - - Examples

11. Filling and Grouping - - Examples​

In this insertion, we solve a few maps to illustrate the straightforward application of the rules. First, we look at the example listed in insertion #8.

f = A"B"C"D" + AB'C'D' + A'BC'D' + A'B'CD' + AB'CD' + A'BCD' + A'B'CD + AB'CD

This has eight terms, all of which are minterms, so these can be entered directly into the map. This is accomplished by putting each minterm into the map cell who's position intersects the corresponding variable states. Thus, the first term in "f" goes into the first cell (# 0), the one which intersects the variables A', B', C' and D' (See rule # 1). The rest are entered in the same way, as shown on figure 20-a.

We then look for cells to collect into a group, while obeying all pertinent rules concerning grouping. By encircling cells numbered "0", "1", "4" and "5", we create a grouping that complies with all rules that are relevant (rules numbered 3, 4, 9, 10, 11 and 14), as is seen in figure 20-a. We then form three more groupings which also corellate to those rules(also shown in figure 20-a). Taken together these groupings also corellate to rules 12, 13 and 15, indicating that the groupings are valid.

When we then evaluate the groupings for the purpose of minimization, we see that each grouping contains four cells, meaning that two variables will be eliminated from each of them. Taking that first grouping (cells 0, 1, 4 and 5), we see that it symmetrically straddles the axis between "A " and "A' ", and the axis between "C' " and "C' ", so that by rule 19, these two variables are eliminated. On the other hand, this grouping intersects "D' ", but does not intersect "D", so that according to rule 20, "D' " is included in this term; and for similar reason, "B' " is included, (Rule 6 is verified) - - - yielding term "B'D' ". Then, similar examination of the other two groupings, gets us the terms "A'D' " and "B'C ", so that we end up with:

f = A'D' + B'C + A'D

Using the same processes, if we start with the following function:

f = ABC' + A'BC' + A'B'C + AB'C + ABC

- - we can put it into a map and group terms as is shown in figure 20-b, using much the same processes as were used in the last example. Note, that this example has only three variables, so that only the top half of a map is used. Solving this map, we get:

f = AB + BC' + B'C

Note, then that from figure 20-c, we can solve the same function, and get:

f = AC + BC' + B'C

- - - and this verifies rule 16.

Next, in figure 20-d, we start with a function that has Eight four-variable terms, and end with two two-variable terms:

f = A'B + AC'

This function is minimized in the same way as before.

Finally, if we are given the following function:

f = AC'D' + B'CD' + BCD' + A'CD + ABD + AB'C'D' + AB'C'D

We immediately see that this is a four-variable function, and that also five of its six terms must be expanded to get a function containing minterms only. When we do so, we get:

f = AB'C'D' + ABC'D' + A'B'CD' + AB'CD' + A'BCD' + ABCD' + A'B'CD + A'BCD + ABC'D + ABCD + AB'C'D

This function is shown entered into each of the maps of figure 21. Comparison of "a", "b", and "c" of figure 21, shows three different, but all correct, groupings for this map, all leading to different but corresponding solutions. These are:

f = AD' + AC' + AB + A'C (figure 21-a)
f = AC' + BC + CD' + A'C (figure 21-b)
f = AD' + BC + AC' + A'C figure 21-c)

The last (figure 21-d) is incorrect because it does not adhere to rule 13.

KM

 

[Kenneth Mann]

12. What Is Wrong - - - If Anything?

12. What Is Wrong - - - If Anything?​

In this insertion, we study the rules given before - - with a few examples. Some, if not all of these in figure 22, are examples of mistakes in the use of the rules.

The example in figure 22-a, is incorrect, because, as shown, the two top circled areas are taken together, and as such violate rule 10. These two are not symmetrical across either the axis between B'-B, or the axis between A-A', and thus cannot be taken together . (In addition, in standard maps of four variables or fewer, all cells "circled" must be adjacent to each other.) In the future, for maps larger than four variables, we'll use different colors to show different groupings, for sake of clarity. The resultant function would be: f = AB'D' + A'B + A'D.

The example in figure 22-b, is incorrect. It violates both rule 10, and rule 4. The correct grouping must consist of two groupings, one including the the four leftmost marked cells, - - and the other, an overlapping grouping including the four rightmost cells. The resultant function would be: f = AC + BC.

The example in figure 22-c, is incorrect. It violates rule 14. A correct grouping would have three groups, one circling the top four cells, one circling the top two and the bottom two and one circling the entire left column. The resultant function would be: f = A'B' + B'C' + B'D'.

The example in figure 22-d, is incorrect. It ignores rule 3. If that rule had been followed it would be recognized that all four cells form an adjacent and symmetrical grouping. The resultant function would be: f = A'C'.

The example in figure 22-e, is incorrect. The vertical grouping shown violated rule 10 and rule 4. The correct grouping would have two groups. These would have; one group containing the top two marked cells and one group containing the bottom two marked cells. The resultant function would be: f = ACD' + AB'D.

The example in figure 22-f, is incorrect. It violates rule 15. There should be only four groupings (and thus four terms). One correct grouping would have; one group containing the two cells in the left (A'B') column, one group containing the two cells in the next-to-left (AB') column, one group containing the two cells in the next-to-right (AB) column and one group containing the two cells in the right (AB') column. The resultant function would be: f = A'B'C' + AB'D' + ABC + A'BD.


The example in figure 22-g, is correct.

The example in figure 22-h, is incorrect. It violates rule 11 and ignores rule 12. The circle enclosing the AB'CD' cell should also contain the top two cells of the first column and the top cell of column two. The resultant function would be: f = A'B' + C'D' + B'D'.

The example in figure 22-j, is correct. This example illustrates the correct observation of rule 3 that was missed in example 22-d.

KM

 

[Kenneth Mann]

13. More Grouping Examples

13. More Grouping Examples​

Following are four examples of the minterm entry, grouping for minimization and reading process:

1) Given the following function:
f = ACD' + BC'D' + ABC'D + A'BC'D + A'B'CD'
- - we expand this to get the following minterms:
f = ABCD' + AB'CD' + ABC'D' + A'BC'D' + ABC'D + A'BC'D + A'B'CD'
we put these into the map to get what is in figure 23-a, and this is grouped and read out to get:
f = BC' + B'CD' + ABD'
Note, that this is not the only possible solution function.

2) Given the following function:
f = A'BC'D' + ABCD' + AB'CD + A'B'C'D
- - we see that, since each of these already has four variables, they are all already in minterm form, so they are entered directly into a map, as shown in figure 23-b. Upon examining this map, we can also say that no grouping can be done, so that this function is already the most reduced form possible.
f = A'BC'D' + ABCD' + AB'CD + A'B'C'D

3) Given the following function:
f = A'B'C'D' + AB'C'D' + ABC'D' + AB'C'D + ABC'D + A'BC'D
- - we see that, since each of these already has four variables, they are all already in minterm form, so they are entered directly into a map, as shown in figure 23-c, and this is grouped and read out to get:
f = AC' + B'C'D' + BC'D

4) Given the following function:
f = A'B'CD' + A'B'CD + ABCD' + ABCD
we see that, since each of these already has four variables, they are all already in minterm form, so they are entered directly into a map, as shown in figure 23-d, and this is grouped and read out to get:
f = A'B'C + ABC

KM

 

[Kenneth Mann]

14. The "Don't Care Condition

14. The "Don't Care Condition​

Often, when we are designing new functions, the input signals, are constrained as to what combination of states will be received. As an example, there could be a system with four machines configured so that no more than two could be running at a time, and our logic could produce its output depending upon which of these is operating or off. Right off, there are certain constraints - - - conditions we don't have to deal with. We could show these conditions with a truth table, representing the machine state outputs by "A", "B", "C" and "D", as follows:

Machine output - - - - D - - C - - B - - A
- - - - - - - - - - - - - - - -0 - - 0 - - 0 - - - 0
- - - - - - - - - - - - - - - -0 - - 0 - - 0 - - - 1
- - - - - - - - - - - - - - - -0 - - 0 - - 1 - - - 0
- - - - - - - - - - - - - - - -0 - - 0 - - 1 - - - 1
- - - - - - - - - - - - - - - -0 - - 1 - - 0 - - - 0
- - - - - - - - - - - - - - - -0 - - 1 - - 0 - - - 1
- - - - - - - - - - - - - - - -0 - - 1 - - 1 - - - 0
- - - - - - - - - - - - - - - -0 - - 1 - - 1 - - - 1 - - - - - Not allowed
- - - - - - - - - - - - - - - -1 - - 0 - - 0 - - - 0
- - - - - - - - - - - - - - - -1 - - 0 - - 0 - - - 1
- - - - - - - - - - - - - - - -1 - - 0 - - 1 - - - 0
- - - - - - - - - - - - - - - -1 - - 0 - - 1 - - - 1 - - - - - Not allowed
- - - - - - - - - - - - - - - -1 - - 1 - - 0 - - - 0
- - - - - - - - - - - - - - - -1 - - 1 - - 0 - - - 1 - - - - - Not allowed
- - - - - - - - - - - - - - - -1 - - 1 - - 1 - - - 0 - - - - - Not allowed
- - - - - - - - - - - - - - - -1 - - 1 - - 1 - - - 1 - - - - - Not allowed

As we can see, there are five combinations of states (0n-off) of the four machines that we will not see, because they are already constrained so as to not operate in those combinations. Because of that, we can more-or-less ignore those states, or even better, handle those states to our own advantage, in our designs. In other words, we can treat them in our designs, to contribute to our logic either as an "occurrence" or as a "non-occurrence", because we'll never have to deal with them. In other words, we can treat them as either "ones" or "zeros" on our map.

These constrained states we call "don't care" states, and as convention, we can represent them as the letter "N" on our maps. Then when grouping our terms, we can choose to either 'include' or to 'not-include' each of them, depending upon which is advantageous to our design - - whichever makes the design simpler.

One word of caution should be voiced here. Whichever way we choose to configure our design, that is how our logic will behave overall - - - so if the "not allowed" should occur, our logic will then define how our circuit behaves. In the real world we should check for contingencies, and determine what would happen if the 'unthinkable' should occur. Usually this won't be a consideration in our design, simply because, in such a case, things will already have gone wrong, and our curcuit won't generally make it any more wrong - - - but we should still check after designing, to make sure. Some sort of recovery might be in order (like with clocks when the power blinks out), but this is usually included in our 'start-up' circuit.

The 'don't care' condition is a powerful design tool, which should prove helpful in many occasions.

KM

P.S: With this insertion I have included an eight-variable map, for general use.

 

[Kenneth Mann]

15. "Don't Care" Examples

15. "Don't Care" Examples​

The following examples, shown in figure 24, use the same four functions as were used in insertion 13, however in this case, certain minterm positions are also assumed to represent "don't care" cases.

1) We were given the following function:
f = ACD' + BC'D' + ABC'D + A'BC'D + A'B'CD'
- - and we expand this to get the following minterms:
f = ABCD' + AB'CD' + ABC'D' + A'BC'D' + ABC'D + A'BC'D + A'B'CD'
We are also given the following "don't care" cases:
N = A'BCD' + A'BCD + ABCD
The expanded function minterms are entered into the map. Also, the "don't care" cases are already in minterm form, so these are entered directly into the map. What we get is shown in figure 24-a. In this case, we choose to treat all the "don't care" minterms as function minterms, because they greatly simplify the solution. What we then get is:
f(N) = B + CD'

2) We were given the following function:
f = A'BC'D' + ABCD' + AB'CD + A'B'C'D
- - and since as we saw before, each of these already has four variables, they are all already in minterm form, so they are entered directly into a map. No grouping can be done, so that this function is already the most reduced form possible, unless "don't care" terms are available.
f = A'BC'D' + ABCD' + AB'CD + A'B'C'D
We are also given the following "don't care" cases:
N = A'B'C'D' + AB'CD' + ABCD + A'BC'D
These are also already in minterm form, and so are also entered directly into the map, and what we get is the map shown in figure 24-b. Now, we can group terms and reduce the resultant function, as shown in the figure, and we get:
f(N) = A'C' + AC

3) We were given the following function:
f = A'B'C'D' + AB'C'D' + ABC'D' + AB'C'D + ABC'D + A'BC'D
- - and since each term here already has four variables, they are all already in minterm form, so they are entered directly into a map. We are also given the following "don't care" conditions:
N = A'BC'D' + ABCD' + AB'CD + A'B'C'D
These are entered into the map along with the function terms, and we get what is shown in figure 24-c. Now, we can group terms and reduce the resultant function, as shown in the figure, and we get:
f(N) = C'
Note that, in this case, we chose to use some of the "don't care" terms and to not use others. That is totally our discretion.

4) We were given the following function:
f = A'B'CD' + A'B'CD + ABCD' + ABCD
and these were already in minterm form, and so were entered directly into the map, as was previously shown in figure 23-d. We were also given the following "don't care" terms:
N = AB'
- - which, when expanded gives us the following minterms:
N = AB'C'D' + AB'C'D + AB'CD' + AB'CD
These terms, when entered into the map along with the function terms, gives us the discretion to form the groupings shown in figure 24-d. From this grouping, we get the following:
f(N) = B'C + AC

Hopefully, these examples help to illustrate how the "don't care" can be used to help simplify the logic design operation. It must be remembered, however that by taking advantage of these constraints, we are actually designing a circuit that operate as planned only if the constraints are not violated. (This is a generally safe assumption, because whatever will violate the constraints would also cause problems in any case. It is still prudent to check for contingency situations after the circuit is designed.)

KM

 

[Kenneth Mann]

16. Maps Larger Than Four-Variables - - - Part 1

16. Maps Larger Than Four-Variables - - - Part 1​

The rules concerning Karnaugh Maps, which we have already discussed, apply to maps larger than four-variables just as they do the smaller ones. The only noticeable difference in handling is the fact that groupings that are combined in the larger maps can now be non-contiguous (as long as they continue to obey the symmetry rule [rule 10]). To make it a bit more methodical, we establish something of a protocol for solving maps of greater than four variables:

1) Start each grouping at its smallest size at first, and build it up (mentally), via a "coupling" process.
2) When coupling two cell groups, every cell within one group must couple to a symmetrically situated cell in the other group.
3) When coupling four or more rows or columns (must be a power of two), start by coupling the two "innermost", then the two "next-to-innermost", etc., until the "two outermost are coupled - - - or at least one pair cannot be coupled.
4) Remember that, because of the "unfolding" way our maps are built, any two adjacent cells will couple. Also, remember that any two cells that are "symmetrical" will couple. The same holds for "groupings", thus any two adjacent or "symmetrical" groupings of the same size will couple, to form the next larger grouping.
5) Each time a larger grouping is formed, by coupling, one variable is eliminated.
6) Remember that, groupings must contain exactly 2^n cells, so that by starting with the smallest size and building the grouping up via coupling, this rule is maintained.

We can use this protocol for building up a grouping, with the filled-in maps of figure 25-a as an illustration. Starting with cells [9,11,25,27], we see that "9" and "11" can be coupled (and eliminate variable "B",as the arrows below the group indicate). The same is the case for "25" and "27". Next we can take the two groupings we have just formed, couple them, and eliminate variable "E".

Then we can do the same thing with cells [15,13,31,29] again eliminating "B" and "E". Next, we notice that the two 4-cell groupings that we have formed are themselves symmetrical about the axis from "C' " to "C", so that these two groupings can now be coupled (and eliminate "C").

Then we can do the same things with cells [57,59,41,43] and cells 63,61,47,45], again eliminating "B" and "E" (two more times), and then couple these two groupings (again, eliminating "C"). Finally we see that the upper grouping and the lower grouping that we have just formed, are themselves symmetrical about the axis from "F' " to "F", so that these can be coupled (eliminating "F"), and we end up with a 16-cell grouping, which has four variables eliminated from it, leaving [f = AD].

In the second illustration of figure 25 (25-b), we can first form the couplings to eliminate "A", then couple each of these horizontally, to eliminate "C". Next, we can couple each of these 4-cell groupings vertically to its adjacent grouping, to eliminate "D", and get two 8-cell groupings. Finally, we couple these two 8-cell groupings, eliminating "F", and end up with a 16-cell grouping. What we then get is [f = BE].

In figure 26, we can follow the same procedure to get [f = C'D'] and [f = AB]. We leave it as a practice exercise to do the same for figure 27.

This is all a straightforward operation, except for one thing - - - how do we determine whether two cells or two cell groups are symmetrical in these larger maps?


KM

 

[Kenneth Mann]

17. Maps Larger Than Four-Variables - - - Part 2

17. Maps Larger Than Four-Variables - - - Part 2​

The main problem with larger maps is - - - determining what is symmetrical? With four-variable maps, all we have to know about any two cells is - - - if they are adjacent they are symmetrical, and if they are symmetrical they are adjacent. With larger maps, it's not quite that simple. Obviously, any two adjacent cells are still symmetrical, but now, cells can be non-adjacent and also be symmetrical. On the other hand a lot of non-adjacent cells are not symmetrical to each other.

To answer this question in the simplest, most straightforward way, figure 28 is included. This figure defines which cells across any horizontal row are "symmetrical" to which other cells along that row. The first illustration (figure 28-a) shows us the obvious, that all cells are symmetrical to their immediate neighbors. Figure 28-b shows us which cell pairs (other than the adjacent ones) are symmetrical within each half - - the left or the right - - of the map. In this case, there are two possible symmetrical couplings (four, if the two adjacent ones in the middle of each half are counted, but these have already been considered as being adjacent). Finally, figure 28-c shows us which cells are symmetrical between the two horizontal halves of the map (again, the adjacent coupling possibilities have been omitted). We can verify these non-adjacent symmetries via either of two methods: 1) study of the "unfolding" process through which the map was formed, or 2) observation of the binary value of the cell numbers, and that only one bit is different between any two symmetrical cells. The same coupling considerations are true vertically.

In figures 29 and 30, we have four cases, in which we shall determine whether 16-cell groupings can be made . In figure 29-a, there are two groupings of eight cells each, with both arranged vertically in columns. Obviously, each column can itself be grouped, since all cells within each column are symmetrical to that column's other cells (because they are all adjacent). The two columns themselves, however are not symmetrical, and thus cannot be combined to form a 16-cell grouping.

In figure 29-b, we cannot create full groupings either vertically or horizontally. Taking the top row, the reason for this horizontally can be ascertained in two ways: 1) The first two cell minterms will couple, as will the last two, but then the remaining two terms will not couple, because they have different variable sets. 2) The simplest way to state it, however is - - that where the cells [19,18] will couple because they are symmetrical, the other cell pair [17,22] will not couple with the first pair because the two pairs are not symmetrical. The same problem exists vertically.

In figure 30-a, there are two 8-cell groupings, but these will not couple because neither the inside columns, nor the outside columns are symmetrical with each other.

In figure 30-b, the cell groupings will not couple either verticlly nor horizontally. In both of these cases, the reason is the same that it was in the figure 29-c case.

KM

P.S: In the maps that have been supplied, the "axes" for any given variable have been 'color matched' to the header block area for that variable. Thus the "axes" between [A'-A] or [D'-D] are black. Likewise, the "axes" between [B'-B] or [E'-E] are blue. Likewise, the "axes" between [C'-C] or [F'-F] are red. This is done to make it a bit easier to determine which variable is being eliminated by a coupling.

 

[Kenneth Mann]

18. Maps Larger Than Four Variables - - Part 3

18. Maps Larger Than Four Variables - - Part 3 - - Recognizing The Patterns​

In the previous two insertions, we have tried to show where and why symmetries exist. Ths simplest and most atraightforward consideration, however is to simply remember the various patterns of symmetry. To do this, figure 31 is included, which shows the predominant cases.

Full-column symmetry corresponding to that of figure 28-c is given in figure 31-a. In each of these cases, 32-cell symmetries are shown. Obvious subsets of these would be symmetrical (2^N) partial rows or partial columns.. Thus, for example, from figure 31-a, we could have just the first two rows, or the second and third - along with the sixth and seventh rows, or maybe the middle four rows. (Where there are symmetries, the intersection of these symmetries are also valid.) Similar, full row symmetry is shown in figure 31-b.

Full-row symmetry corresponding to that of figure 28-b is given in figure 31-c. The same variations hold as in the paragraph above. Similarly, for that shown in figure 31-d.

A couple of the many adjacent-cell symmetries, as laid out in figure 28-a, are shown in figures 31-e and 31-f. Finally, it is pointed out again that any intersection of these symmetries is valid. Thus, for example we could intersect the symmetries of figure 31-a with those of figure 31-d, and get a pattern of cells [1,3,7,5,17,19,23,21,49,51,55,53,33,35,39,37]. The trick here is to see all of the myriad possibilities.
(One possibility here is to make a set of transparent overlays.)

A few example cases are shown in figure 35. Fir each of the four cases, which, if any of these groups can be combined to form a 16-bit cell group?

KM

 

[Kenneth Mann]

19. The Eight-Variable Map

The number of variables in a symmetrical, reflecting K-Map, is limited only by the size that a person is willing to draw, and the complexity of the patterns that one is willing to delve into. We have included in this series, an eight-variable map, so a few words are given here.

Figure 32 shows three (of the four) types of symmetry pattern that might exist with the eight-variable map (adjacent cell symmetries are not shown - - these should be obvious). In general for every two variables added to the map, another two levels of symmetries are also included, one for vertical and one for horizontal.

Figures 33 and 34 show just a few of the symmetry patterns possible from the types revealed in figure 32.

KM

Answer to the question of insertion 18: Only "d" is combinable to form a 16-cell group.

 

[Kenneth Mann]

20. The Truth Table

20. The Truth Table​

To begin, we introduce here the idea of the "designation pattern", as was first used by M. Mahoney (he called it a designation number). To avoid undue confusion, we will not use it as extensively here, but only to introduce the "truth tables" concept. (Actually, it can be used to demonstrate many basic concepts of Boolean logic, but that is beyond the scope of this series.

Basic the "designation number" is nothing more than an arbitrary series of ones and zeros used to represent a variable. Virtually any pattern can be chosen for each variable, however there as a preferred choice. In addition the bit length of the designation patterns is determined by the total number of variables being handled, such that, if there are "N" variables, each will have 2^N bits in its designation pattern. The preferred representation is:
0101 0101 01... for the first variable being represented
0011 0011 00... for the second variable being represented
0000 1111 00... for the third variable being represented.
0000 0000 11... for the fourth variable being represented.
etc.

Thus if we have three variables "A", "B", and "C", then these would be represented by a designation pattern as follows:
#A = 0101 0101
#B = 0011 0011
#C = 0000 1111

The advantave to this arrangement is that it allows the truth values (or "YES" and "NO") to be represented by normally numerical symbols ("0" and "1") while still understanding that these are in a Logical, not an Arithmetic context. Thus we would have the following representations:
A' -> 0, and A -> 1
B' -> 0, and B -> 1
C' -> 0, and C -> 1; in our designation patterns.

If we then take our group of designation patterns, as shown above, and rotate it clockwise 90-degrees, we would have:
C - B - A
0 - 0 - 0
0 - 0 - 1
0 - 1 - 0
0 - 1 - 1
1 - 0 - 0
1 - 0 - 1
1 - 1 - 0
1 - 1 - 1

And this is the exact arrangement we have in our truth tables (as were supplied earlier). Note that the first variable (usually "A") here is to the right. This allows us to deal with our truth table entries as if they were binary numbers rather than the logic values that they actually are. This makes handling their values easier, in fact, we can represent each of the rows of the "designation stack" that we have created, by its decimal equivalent (as is done in the supplied truth tables). The use of the truth tables makes it easier to handle and keep track of what we are doing in the large majority of cases, especially the non-trivial ones, and especially when we are designing the logic to perform some numerical or arithmetic function.

KM

 

[Kenneth Mann]

21. Using The Truth Table

21. Using The Truth Table​

Use of the truth table greatly simplifies the process of getting data into the map and lessens the chance for entry error. It gives us an information entry guide. First of all, if we enter data directly into the map, we are forced to account for the logic minterms which are to be entered, and then to try to match these up with the graphical architecture of the map. (For example, where is the A'B'CD' intersection? By the time we find its map location we may have forgotten the exact Alphabet representation. Then we have to go back and double-check, and retrace the map cell we have found back to its headers to verify correct variable states. In some cases, it might even be advisable to pencil in each minterm into the selected cell in order to be able to check it for correctness.)

In the truth table, we would simply match the "Yes" - "No" status of the letter representations to the "0" - "1" status of the map, and make entries into the matching column/row position of the selected output function.

This advantage is especially pronounced when we are dealing with logic that we are designing to generate some sort of numeric function outputs (like adders counters and the like). Then we simply mark the function output wherever we have the desired numerical input condition values.

Then, when we have our truth table annotation finished, we simply transfer the information directly to the map(s) by simply using the decimal values in the "NUM" column to locate the corresponding map cell (where all cells are numbered). We then solve the map in the usual way.

KM

 

[Kenneth Mann]

22. Truth Table - - - Use Example

22. Truth Table - - - Use Example​

For a simple example, we are given the following set of terms, and asked to solve for the minimum.

W = A'BC'D' + A'BC'D + ABC'D' + ABC'D + AB'C'D' + AB'C'D + A'BCD' + A'BCD

To make this a bit easier to handle, it is suggested that the order of the variables of each term first be reversed:

W = D'C'BA' + DC'BA' + D'C'BA + DC'BA + D'C'B'A + DC'B'A + D'CBA' + DCBA'

Then, as the next step, we substitute "0" and "1" values for each variable, according to whether it is in its "negated" or its "asserted" state:

W == 0010, 1010, 0011, 1011, 0001, 1001,0110, and 1110

And then we assume these to be binary values, and substitute for them their decimal equivalents:

W == 2, 10, 3, 11, 1, 9, 6, and 14

Then, for each of the decimal values above, we enter a mark in that position on the truth table, as is shown in figure 36. (In the figure, stars (*) were used, but this was done only to make it reproduce clearly. Normally ones (1), or the like would be used.)

Next, taking the decimal values from the truth table "NUM" column, each corresponding position in the map is marked as is shown in figure figure 37. The map is then solved, and we get the following terms:

W = AC' + A'B

The resulting functional circuit for this is shown in figure 38-a, and its practical equivalent if, for example, implemented in TTL, is like that shown in figure 38-b.



NOTE 1: This is a simple case. Careful examination of the original equation would reveal to us that the "D" terms could have been immediately dropped out, and it could then have been solved as a three-variable problem. This will not always be readily apparent, however and it is thus advised that the cases be handled as done.

NOTE 2: It is here observed that functions to be solved, like "W" above, can also be expressed as "designation patterns" just as is each variable, thus as its designation pattern we would have had:
#W = 0111 0010 0111 0010
(This is simply the marked "pattern" that is entered under "W" in the truth table.) It is simply another way of representing the minterms of the logic statement.

KM

 

[Kenneth Mann]

23. The Design Process

23. The Design Process​

Now, it is time to devote effort to the way of creating actual working logic functions using Karnaugh Maps. The method laid out is intended to "automate" much of this process. A block diagram for the process is shown in figure 39*.

The dynamics of the process are as follows:

1) We first produce a word description of the end product (the module/black box). In that description we try to define everything about the product; the inputs available, the output(s) needed, and how the inputs (and possibly outputs) will be combined to generate the output(s).

2) From the original statement of the problem, and using the relationships and rules that are generated, produce a "pseudo module", a simple block diagram which adequately describes the operations and relationships. Show all inputs and outputs, and describe the relationships between these.

3) Use the descriptions and relationships defined to determine what the truth table input "variables" will be, what the output "functions will be, and how these output "functions" will be entered into the truth table.

4) Generate the output function(s) "designation pattern(s)" by defining the relationships developed from the variables to the functions, and marking these into the truth table.

5) When the function(s) has/have been defined, enter the function values from the truth table to one or more Karnaugh Map(s).

6) Solve the K-Map(s) to define the logic that will implement the needed function(s).

7) Derive the basic logic circuitry that will be needed.

8) Refine the design to produce the actual circuitry that will be used.

The types of circuit that we deal with using this technique include essentially the following:

Combinatorial: Note, that all logic circuits are, in some way, combinatorial. By combinatorial here, we refer to those that are not sequential.

Sequential: A (combinatorial) logic circuit which has a memory element(s) which, along with (maybe) some or all of the inputs to the circuit, determine the (output) states of that circuit. Sequential circuits are further divided into:

Asynchronous: Sequential logic that is not synchronous, and which depends usually upon built-in delays for the needed memory/feedback signals. These circuits can, at times, be unstable.

Synchronous: This includes sequential logic whose behavior is defined by the state of its input and feedback signals at discrete instants of time. It is in most cases, clocked. Its memory elements are usually flip-flops. In this class of sequential logic we usually also include those devices termed as State Machines.


KM

* Adapted from a process given by M. Mahoney.

 

[Kenneth Mann]

24. Combinatorial Circuit Example - - - Trinary System Adder Element​

This is an intriguing little application. I cannot give a use for it right offhand, but I find it interesting. Basically it is a Trinary/Ternary system (base three) adder element (similar to a binary full adder, the basic distinction being that where the binary full adder adds two single-bit values and a carry, this adds two two-bit quantities and a carry). Essentially, when we compare trinary numbers to decimal, etc., we have something like:

Decimal - - - - - - - - - - Trinary - - - - - Binary Coded Trinary
00 - - - - - - - - - - - - - - - 000 - - - - - - - - - 00 00 00
01 - - - - - - - - - - - - - - - 001 - - - - - - - - - 00 00 01
02 - - - - - - - - - - - - - - - 002 - - - - - - - - - 00 00 10
03 - - - - - - - - - - - - - - - 010 - - - - - - - - - 00 01 00
04 - - - - - - - - - - - - - - - 011 - - - - - - - - - 00 01 01
05 - - - - - - - - - - - - - - - 012 - - - - - - - - - 00 01 10
06 - - - - - - - - - - - - - - - 020 - - - - - - - - - 00 10 00
07 - - - - - - - - - - - - - - - 021 - - - - - - - - - 00 10 01
08 - - - - - - - - - - - - - - - 022 - - - - - - - - - 00 10 10
09 - - - - - - - - - - - - - - - 100 - - - - - - - - - 01 00 00
10 - - - - - - - - - - - - - - - 101 - - - - - - - - - 01 00 01
11 - - - - - - - - - - - - - - - 102 - - - - - - - - - 01 00 10
12 - - - - - - - - - - - - - - - 110 - - - - - - - - - 01 01 00
... - - - - - - - - - - - - - - - ... - - - - - - - - - - ...
... - - - - - - - - - - - - - - - ... - - - - - - - - - - ...

The trinary adder that is envisioned would have five input signals (two 2-bit values being added, and a single bit "carry in" as is shown in figure 42, the "pseudo module" for the adder. This module would comply to the following addition rules:

With no carry-in (value = "0") we get:
Addend - - - - - - - Augend - - - - - - - - Sum/Carry Out
- - - 00 - - - - - - - - - - 00 - - - - - - - - - - - 00 / 0
- - - 00 - - - - - - - - - - 01 - - - - - - - - - - - 01 / 0
- - - 00 - - - - - - - - - - 10 - - - - - - - - - - - 10 / 0

- - - 01 - - - - - - - - - - 00 - - - - - - - - - - - 01 / 0
- - - 01 - - - - - - - - - - 01 - - - - - - - - - - - 10 / 0
- - - 01 - - - - - - - - - - 10 - - - - - - - - - - - 00 / 1

- - - 10 - - - - - - - - - - 00 - - - - - - - - - - - 10 / 0
- - - 10 - - - - - - - - - - 01 - - - - - - - - - - - 00 / 1
- - - 10 - - - - - - - - - - 10 - - - - - - - - - - - 01 / 1

And with a carry-in (value = "1") we get:
Addend - - - - - - - Augend - - - - - - - - Sum/Carry Out
- - - 00 - - - - - - - - - - 00 - - - - - - - - - - - 01 / 0
- - - 00 - - - - - - - - - - 01 - - - - - - - - - - - 10 / 0
- - - 00 - - - - - - - - - - 10 - - - - - - - - - - - 00 / 1

- - - 01 - - - - - - - - - - 00 - - - - - - - - - - - 10 / 0
- - - 01 - - - - - - - - - - 01 - - - - - - - - - - - 00 / 1
- - - 01 - - - - - - - - - - 10 - - - - - - - - - - - 01 / 1

- - - 10 - - - - - - - - - - 00 - - - - - - - - - - - 00 / 1
- - - 10 - - - - - - - - - - 01 - - - - - - - - - - - 01 / 1
- - - 10 - - - - - - - - - - 10 - - - - - - - - - - - 10 / 1

We then enter these values into our truth table, just as they appear in the table above, where:
1) D and C are the "variables" for the addend.
2) B and A are the "variables" for the augend.
3) E is the variable for the carry in.
4) Y and X are the functions for the sum.
5) Z is the function for the carry out.
These are entered into the table where the variables match the binary values of the table. We notice first, that the table values go in directly; with no need to convert from minterms. We also notice that some binary values of the truth table do not occur in the trinary systen (ie. where the value "11" occurrs, because there is no "three' in the trinary system), so in those places we put "N" for "don't care. The map, when filled, looks like that in figure 40.

The values from the truth table are then entered, by-the-numbers, into our K-Maps, as is indicated in figure 41. There are three maps, because we have three functions (X, Y and Z). When these three maps are then solved we might get the following minimized functions:

X = AC'D'E'F' + A'B'CE'F" + BDE'F' + AC'DEF' + BCEF' + A'B'C'D'EF'
Y = BC'D'E'F' + ACE'F' + A'B'DE'F' + AC'EF' + A'B'CEF'
Z = BCF' + AC'DF' + BDF' + DEF' + A'BEF' + ACEF'

KM

 

[Kenneth Mann]

25. Combinatorial Circuit Example - - - 3 X 3 Multiplier - - - Part 1

25. Combinatorial Circuit Example - - - 3 X 3 Multiplier - - - Part 1​

In this example, we create a simple binary multiplier, not part of an arithmetic unit, but one to be able to multiply two signals or controls, or to serve as part of a modulating function etc. It will take two three-bit input signal lines and multiply these, putting the output on a six-bit output line. This permits an output from zero to 49, derived using 6-variable maps. If a greater range had been desired, an eight-variable map would have given a 0-225 range, or a ten-variable map would yield a 0-961 range.

The basic pseudo module for this circuit is shown in figure 43. From it we can assume variables "A", "B" and "C" to form the multiplicand, and "C", "D" and "E" the multiplier. (Or you can swithc them around if you desire.) It uses our standard multiplication table (expressed in binary), so we can just plug the values right into the truth table. We get that which is shown in figure 44. From that, we enter each function ("P", "R", "S", "T", "V" and "X") into its own K-Map. The first four of these are shown in figure 45, along with possible solutions. The remaining maps will be shown in the next insertion.

This is a good place and occasion to practice solving a larger-than-four-variable map, so we shall attempt to do so here. Starting with figure 45, and the map for the variable ""P", we see that all the cells on it that are marked, representing a minterm presence - - - can be represented into just one grouping (circled with green). It represents a good example of what a valid non-adjacent group looks like. It contains some of the symmetries that were described, and when read out, the only variables that are not eliminated are "A" and "D", thus we get "P = AD ". Other maps are solved as follows:

The second map gives us minimized values for "R". This one works out to four minimized terms, all represented by non-adjacent groupings, and each grouping enclosing eight minterms - - before minimization is done. These include: 1) circled in 'red" - BDE'; 2) circled in blue - A'BD; 3) circled in green - AB'E and 4) circled in "black" - AD'E.

The third map encompasses nine minimized terms. These are: 1) in dotted green - A'CDE'; 2) in dotted black - ACDF'; 3) in orange - A'B'CD; 4) in green - A'BC'E; 5) in blue - BD'EF'; 6) in dotted red - A'BD'E; 7) in purple - AB'D'F; 8) in black - AC'DF and 9) in red - AD'E'F.

The fourth map encompasses ten terms, two of which cannot be minimized, and thus weren't circled, but must be accounted. These terms are: 1) in the upper red - B'CEF'; 2) in the upper orange - A'B'CE; 3) in dotted blue - CD'EF'; 4) in green - ACD'E; 5) in blue - A'BC'F; 6) in dotted green - A'BDF; 7) in the lower orange - BC'E'F 8) In the lower red - BD'E'F; 9) standalone - ABC'DEF' and 10) standalone - AB'CDE'F.

Hopefully, this will help to clarify how larger maps are solved. The remaining maps will be shown and solved in the next insertion.


KM

 

[Kenneth Mann]

26. Combinatorial Circuit Example - - - 3 X 3 Multiplier - - - Part 2

26. Combinatorial Circuit Example - - - 3 X 3 Multiplier - - - Part 2​

The maps for the 3 X 3 multiplier are shown in figure 45 (previous insertion) and figure 46 (this insertion). Going through the remaining two maps (in figure 46), for the first, which represents "V", we get: 1) circled in purple - BCDEF'; 2) circled in dotted red - ABCDE; 3) circled in dotted purple - ABC'EF; 4) circled in green - B'CD'F; 5) circled in red - A'B'CF; 6) circled in black - A'CE'F; 7) circled in orange - B'CE'F and 8) circled in blue - CD'E'F.

For the second map of figure 46, there are three terms, as follows: 1) circled in green - BCEF; 2) circled in red - ABCDF and 3) circled in black - ACDEF.

Remember, that in a grouping, if 2^n cells are circled, then 2 variables will be dropped out of the term represented by that group. Solutions from these maps are as follows:

P = AD
R = BDE' + A'BD + AB'E + AD'E
S = A'CDE' + ACDF' + A'B'CD + A'BC'E + BD'EF' + A'BD'E + AB'D'F + AC'DF + AD'E'F
T = B'CEF' + A'B'CE + CD'EF' + ACD'E + A'BC'F + A'BDF + BC'E'F + BD'E'F + ABC'DEF' + AB'CDE'F
V = BCDEF' + ABC'EF + B'CD'F + A'B'CF + A'CE'F + B'CE'F + CD'E'F + ABCDE
X = BCEF + ACDEF + ABCDF


KM

 

[Kenneth Mann]

27. Sequential Circuits - - Introduction

27. Sequential Circuits - - Introduction​

As described in insertion number 23, a sequential circuit is one which has one or more "memory elements", which (possibly in combination with some or all of the inputs) combine to determine what the (next) output states of the circuit will be. These memory elements accomplish this sequential action by 'retaining for a period of time' what (one or more of) the earlier state conditions were. These are then combined (compared) with each other or with input conditions - - and when certain certain conditions occur, the output states are changed. As was also pointed out, sequential circuits can be either "asynchronous" or "synchronous". The former usually derives its memory via a propagation delay through the circuit, while the latter generally employs "flip-flops" to hold the memorized information.

The most basic such sequential circuit to be examined, is the flip-flop itself. The basic (direct coupled R-S, or latch) flip-flop, shown in figure 47, is itself example of an asynchronous sequential circuit. It gets its memory via propagation delay through the gates. There are two basic constructions, as are shown in figure 47. These are the type made up of NAND gates (sometimes referred to as 'reset dominant'), and the type composed of NOR gates (set dominant). Their operations, though not quite the same are equivalent. We are more accustomed th the type made up of NANDs, so we shall examine this type.

To go through the operation of the first circuit in figure 47, we recall that the output of a NAND gate is "1" as long as either input is "0", and the output will go to "0" only when both (or all) inputs are "1". Thus, if we assume a starting point having both inputs with "1" on them (the quiescent, or non-active state). then the outputs will not be changed from what they already were. To see this, assume that the "Qs" output is "0" and the "Qr" output is "1" (they must always be opposites, except during a brief instant of change). Then, from the "Qs" output, one of the inputs to the "reset-side" gate will have a "0" to it, and thus that gate's output must be "1". This means that the inputs to the other (set-side) gate will have two "1" inputs, and thus its output will be held at "0" (since, as we stipulated, the inputs are both "1"). Then, if we place a "0" (pulse) on the "Rst" input, nothing will happen, because this flip-flop is already in the "1" state, to which such a pulse would have driven it. If, on the other hand, we put a "0" (pulse) on the "set" input, its output will now be driven to "1", at which point, both inputs to the "Rst" side gate would be "1", and thus drive its output to "0", and this is where the 'memory' takes place. As result of the propagation delays through the gates, once the set input goes back (up) to "1", that gate's output will now stay at "1", because the "0" at the other side of the gate will not have had time to change, and now because of two "1" values on the other (rst) gate, it will not be allowed to.

There must always be one 'caveat' involved when using the simple RS flip-flop: the "Set" and "Rst" inputs must never be allowed to both be "0" at the same time. Such an occurrence would put the flip-flop into an unstable state.

Finally, both flip-flop illustrations of figure 47 also show the standard "truth tables" for them, as is usually illustrated with these devices. Here, it is suggested that these truth tables be expanded to show them in a way that is more compatible with our use of tables in the design process. To do this, we introduce a third 'input variable' in the table, along with "Set" and "Rst". This variable is "Qsn-1" , the previous output state of the "Qs" output. (There is no need to represent both outputs, because they are always directly related to each other.) It is suggested that the table be represented in a manner similar to the following:

Set - - Rst - - Qsn-1 - - - - - - - Qs - - Qr
0 - - - 0 - - - - 0 - - - - - - - - - - Not Used
0 - - - 0 - - - - 1 - - - - - - - - - - Not Used
0 - - - 1 - - - - 0 - - - - - - - - - - - 1 - - - 0
0 - - - 1 - - - - 1 - - - - - - - - - - - 1 - - - 0
1 - - - 0 - - - - 0 - - - - - - - - - - - 0 - - - 1
1 - - - 0 - - - - 1 - - - - - - - - - - - 0 - - - 1
1 - - - 1 - - - - 0 - - - - - - - - - - - 0 - - - 1
1 - - - 1 - - - - 1 - - - - - - - - - - - 1 - - - 0

By representing a table in a way similar to this one, the 'previous (or subsequent) states can be used in the mappings.

KM

 

[Kenneth Mann]

28. The J-K Flip Flop

28. The J-K Flip Flop​

Probably the most essential component of the sequential circuit, particularly the synchronous sequential circuit, is the J-K flip-flop. This is the unit most often used to provide the clocked memory needed for these circuits.

The basic R-S flip flop, as was shown in figure 47, can be expanded to allow clocked inputs, by the addition of two gates, as is shown in figure 48. With the inclusion of these two gates, we now have two new inputs "J" and "K", which similarly to the "Set" and "Rst" inputs, can be used to change the output states ("Qs" and "Qr") of the flip-flop. Unlike "Set" and "Rst", however, these "J" and "K" inputs will not switch the flip-flop unconditionally and unclocked, but rather will only do so upon transition (rising or falling, depending on the device used) of the clock signal. The truth table for these signals is as follows:

K - - - - J - - - - Ckt-1 - - - Ckt- - - - - - - - - - Qst - - - - -Qrt
0 - - - - 0 - - - - - 0 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 0 - - - - - 0 - - - - - - 1 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 0 - - - - - 1 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 0 - - - - - 1 - - - - - - 1 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 1 - - - - - 0 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 1 - - - - - 0 - - - - - - 1 - - - - - - - - - 1 - - - - - - 0
0 - - - - 1 - - - - - 1 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
0 - - - - 1 - - - - - 1 - - - - - - 1 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 0 - - - - - 0 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 0 - - - - - 0 - - - - - - 1 - - - - - - - - - 0 - - - - - - 1
1 - - - - 0 - - - - - 1 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 0 - - - - - 1 - - - - - - 1 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 1 - - - - - 0 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 1 - - - - - 0 - - - - - - 1 - - - - - - - - -"undefined"
1 - - - - 1 - - - - - 1 - - - - - - 0 - - - - - - - - -Qst-1 - - - Qrt-1
1 - - - - 1 - - - - - 1 - - - - - - 1 - - - - - - - - -Qst-1 - - - Qrt-1
- Ckt-1 = previous clock value
- Ckt = present clock value


The first thing of note from the table above, is the fact that, since nothing takes place at any time except for the rising edge transition of the clock, it is perfectly acceptable to drop the clock from the table, and to just include a reference note to that effect. This leaves us with the following table:

K - - - - J - - - - - - - - - - Qst - - - - -Qrt
0 - - - - 0 - - - - - - - - - -Qst-1 - - - Qrt-1 Note: The "Q"
0 - - - - 1 - - - - - - - - - - - 1 - - - - - - 0 outputs change only
1 - - - - 0 - - - - - - - - - - - 0 - - - - - - 1 with rising clock
1 - - - - 1 - - - - - - - - - - -"undefined" transition.


The circuit that we have displayed has a couple of drawbacks. First, it has an "undefined" state, something we always like to avoid. The second, is the fact that it has no provision for "toggling the output. We solve both of these problems by providing feedback from the outputs to the input gates, as is shown in figure 49. For this circuit, we have the following truth table:

K - - - - J - - - -Qst-1 - - - - - - - - Qst - - - -Qrt
0 - - - - 0 - - - - 0 - - - - - - - - - - - 0 - - - - - - 1 - - - no change
0 - - - - 0 - - - - 1 - - - - - - - - - - - 1 - - - - - - 0 - - - no change
0 - - - - 1 - - - - 0 - - - - - - - - - - - 1 - - - - - - 0 - - - "set"
0 - - - - 1 - - - - 1 - - - - - - - - - - - 1 - - - - - - 0 - - - "set"
1 - - - - 0 - - - - 0 - - - - - - - - - - - 0 - - - - - - 1 - - - "clear"
1 - - - - 0 - - - - 1 - - - - - - - - - - - 0 - - - - - - 1 - - - "clear"
1 - - - - 1 - - - - 0 - - - - - - - - - - - 1 - - - - - - 0 - - - "toggle"
1 - - - - 1 - - - - 1 - - - - - - - - - - - 0 - - - - - - 1 - - - "toggle"

This circuit is often the device used for the memory in synchronous sequential circuits. Using the "J" and "K" inputs as controls, it can provide for a clocked set, a clocked clear and a clocked toggle.

KM

 

[Kenneth Mann]

29. Synchronous Circuit Example - - - BCD counter

29. Synchronous Circuit Example - - - BCD counter​

This insertion is an application of the K-Map and its accompanying truth table, to the design of a typical synchronous sequential circuit - - - a BCD counter. As such, this unit will involve four J-K flip-flop units, one to hold each bit of the BCD value. It is our task to configure these count elements so that they will sequence properly through the BCD count range. We shall see, that using our approach, this is a fairly simple task.

The basic circuit consists of the four J-K flip-flops that are dedicated to containing our count value, as is shown in figure 50 - - - plus some,as of yet, undetermined logic that will cause the values of our flip-flops to cycle through the BCD values, synchronously, as they receive pulses to their clock inputs. For our purposes, the "set" and "clear" inputs to the flip-flops are not needed, and are thus kept tied to a high input (Vcc) value. Also, the Q' values are not needed and are thus not shown, All of the counting is controlled simply by toggling each of the flip-flops at the proper times, and thus their "J" and "K" inputs are tied together. Whenever we need to toggle them, we put a "1" value on them. Otherwise, we hold them at "0". The circuitry that will control this action is the "counter control module" shown in figure 50. This module takes the "Q" values from the four flip-flops, and from those, determines which flip-flop(s) to toggle at the next clock, and for the one(s) selected, sends a "1" value to the "J/K" input(s).

To determine which flip-flops are to be toggled at each count, and thus to define the logic equations and the resulting logic, we simply observe our BCD count values into the truth table, as is shown in figure 51. In order to know which flip-flop will be enabled to toggle at each count value, we simply observe which ones are to change. Thus, for example, the lowest order flip flop will change at each count (0 to 1 to 0 to 1, etc.) thus that flip-flop will always be enabled. We simply tie it to "1" (Vcc). The "third" flip-flop, on the other hand, will only change value (toggle) on two occasions, when it is at "3" and goes to "4", and when it is at "7" and goes to "8". For each of the four flip-flops (except the first, which is the trivial case), we mark in the truth table where it is about to 'toggle'. Thus, for the second flip-flop (Jb), we mark in five places, for the third (Jc), we mark two places, for the fourth (Jd), we mark two, and for the carry (Co), we mark one place. Thus what we get is the truth table as is filled in in figure 51. Note also that, since this is a BCD counter, values "10" through "15" are not used and thus are marked as "dont-care" values.

The next task is simply to transfer our truth-table entry values into our Karnaugh maps, one for each of our functions (Ja through Jd and Co). In actuality, "Ja" is the trivial case and need not be transferred to the map. What we get then is the maps shown in figure 52. The nice thing about our approach with this example, is the fact that we didn't have to first figure out our initial Boolean terms and translate these to the truth table. We went directly from our count values to the table, putting the values in, more-or-less, by the numbers. The resulting logic for these functions, which will define our circuitry, will be shown in the next insertion.

KM

P.S: Note that where we didn't use the "Set" and "Rst" values here, we have them available if we wish, for such things as manual setting counter, etc.

 

[Kenneth Mann]

30. Synchronous Circuit Example - - - 1 T0 12 Counter

30. Synchronous Circuit Example - - - 1 T0 12 Counter​

First, we note that figure 53 is of the BCD counter developed in the last insertion, but which we did not have space to show there.

Now, we look at a counter which one person wanted to develop a couple of months back. This counter will count up to and include the value "12", but will not include the "0" value. If we want to know where such a counter would be used, we need only look at the standard "hour clock". It starts at the "One Oclock" value, and counts up to and past the "Twelve Oclock" value (though though the values from :"Twelve" to "One" are actually handled as the "Zero" values).

This counter is designed in a way much like that of the BCD counter. Again, four flip-flops are used, and we simply determine where these are to be toggled. Using the truth table the same way as before, it is filled out as is shown in figure 54. (Again, the lowest-order flip-flop simply toggles every time, and as such, is a trivial case and is not included in the truth-table. For each of the other flip-flops, and for the "carry out", we mark the place in the table (before) where the associated flip-flop is to be toggled.
This gives us the 'functions' (Jb, Jc, Jd and Co) which will go to the respective flip-flop J and K inputs, and enable them for toggling at the proper times.

The table values are entered directly into their respectivr Karnaugh Maps, and solved. The maps are shown in figure 55. The logic diagram will be included in the next insertion.

KM

 

[Kenneth Mann]

31. One To Twelve Counter - - Part 2

31. One To Twelve Counter - - Part 2​

The basic logic for the 1-to-twelve counter that we have derived, is shown in figure 56.

One additional caution should always be exercised when designing sequential logic, especially where "don't-care" states are used. We should always check afterward to make sure that no "blip", like a power interruption or line spike can put us into a state from which we cannot get out. Normally, this won't happen, but we should check just to make sure. Obviously, if such a 'blip' occurs, our circuit will be thrown out of sequence; there's nothing we can do about that since logic circuitry is dependent upon its power sources, etc., but we do want to be able to recover afterward.

To check the circuitry we must assume the circuit in every possible state, and trace its actions via the logic diagrams. The "State Diagram" shown in figure 57, shows us where the 1-to-12 counter goes during the transition from each 'state' (count), and thereby we see that this unit will recover on its own, (We already knew by definition where the count would go after each 'allowed state'.) Our state diagram also shows us that this counter is a simple "state machine" (Moore Machine), however that topic we shall consider beyond the scope of this discussion. (As an example, such a discussion would have to factor in the types of flip-flops and their "excitation table" characteristics, and whether there are external inputs, etc.)

KM

 

[Kenneth Mann]

32. Base Six Counter

32. Base Six Counter​

The Counter illustrated in this insertion is configured in the same manner as the others. It is intended to handle count values "0" through "5". Its truth-table is given in figure 58, its Karnaugh Maps are given in figure 59 and its diagram is in figure 60. It is left to the reader to go through the design derivation.

KM

 

[Kenneth Mann]

33. A Time-Of-Day Clock

33. A Time-Of-Day Clock​

This insertion is included simply to give a hint as to how the count modules shown in the previous insertions might be used in a "real world" type application. In other words, this tells us how we might build a twelve-hour clock unit like the ones that been offered at very low cost for the last twenty or more years. Figure 61 illustrates such a clock, and gives us an indication of just how simple it is. It drives simple BCD displays to give us a five-digit seconds-minutes-hours indication, being updated by a once-per-second count. The lowest (leftmost) BCD counter updates once per second and puts out its 'carry' once every ten seconds, This carry goes to the next (base six) counter at each of those ten-second intervals and enables that counter to update. Its output then enables the next (BCD) counter to update every 60 seconds. This is repeated to the final (one to twelve) counter, and its output carry then goes to the (toggle) inputs of a standard flip-flop, which toggles back and forth once every twelve hours, to give us the "AM/PM" indicator. Also shown is a "clock load" circuit block diagram. This may be something as simple as a set of 'advance' buttons similar to what most digital clocks now have; to a moderately more complex 'keypad type entry; to an even more sophisticated interface to WWV (very accurate) or GPS (even more accurate).

KM

 

[Kenneth Mann]

34. Finding SPOS solutions.

34. Finding SPOS solutions.​

It was mentioned earlier (in insertion # 8) that the Karnaugh Map is primarily a tool devised with the aim of obtaining Simple-Sum-Of-Products (SSOP) solutions. As a final topic, we will show here that it can also be used to derive Simple-Product-Of-Sums (SPOS) solutions.

The rules for deriving SPOS solutions are as follows:

1) Determine the basic functions and enter them into maps as we have been doing all along.

2) Group the empty (zero) cells (plus any desired "don't cares"), thus yielding the SSOPs for f ' (f-bar).

3) Determine the SSOP solution terms for f '.

4) Then, to get "f ", complement both sides of the resulting equations.

5 ) Apply De Morgan's Theorems

That's all there is to it. As an example, consider the function with the following minterms:

Y = A'B'C'D' + A'B'CD' + A'B'CD + A'B'C'D + AB'CD'

The Karnaugh mapping would be that shown in figure 62, so when we group the empty cells, we get that shown in figure 63. The resultant SSOP is:

Y' = B + AC'

Y = (B + AC')'
Y = B'(AC')'

Y = B'(A' + C) [I hate using the apostrophe in place of the "overline"]

If we had sought the SSOP solution, the groupings would resemble those of figure 64, and the SPOS solution would be:

Y = A'B' + B'C

In this case, if we factor the SPOS answer we get the same as the SSOP, however the conversion will not always be this easy.


KM