Pendulum Potential energy equation

cres222

hello every one
i have this pendulum:

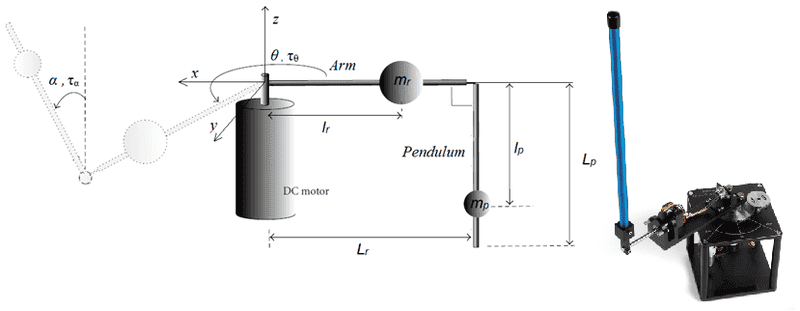
i need to stabilize the pendulum in the inverted position , i need to know the potential energy for the pendulum , i read several articles in each one i have a different equation :
[itex]V=mgl_{p}cos\alpha[/itex]
[itex]V=-mgl_{p}cos\alpha[/itex]
[itex]V=mgl_{p}(1-cos\alpha)[/itex]
[itex]V=mgl_{p}(cos\alpha-1)[/itex]
Now i'am really confused which equation is the correct one?
Please help me

Doc Al

What are you taking as your reference level? (Where PE = 0.) The pivot? The gravitational PE is given by mgΔy, where Δy is measured from your chosen reference level. Using that you should be able to pick the correct formula.

cres222

[itex]P.E=0[/itex] at the vertical position ([itex]\alpha=0[/itex] from the vertical line in the picture above), now which formula should i use :
[itex]P.E=mgl_{p}(1-cos\alpha)[/itex]
or
[itex]P.E=mgl_{p}(cos\alpha-1)[/itex]

Doc Al

Using the vertical position as your reference, Δy will be negative for any nonzero angle. The second of those is the one you want.

cres222

so:
[itex]\Delta y=[/itex](center of mass level-reference level)
not the other way around , am i correct?

Doc Al

Δy is measured from the PE = 0 reference point. Another way to write the PE is mgy, where y is the vertical position of the center of mass and y = 0 is the PE = 0 point.

Since you are choosing the reference level to be where the pendulum is vertical (the angle is zero) and thus the mass is at its highest point, all values for y and thus PE for non-zero angles will be negative since they are below that point.

cres222

Now i understand , thank you very much for you kindly help,I'm very appreciative