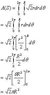Derivation for formula of area of a cone

[irodus]

Homework Statement

Consider a cone of height H and base radius R with its apex (tip) at the origin, and its base at circular end at z = H.
Derive the equation for the surface of the cone in cylindrical coordinates. You may assume z is proportional to r.

Homework Equations

I assume the formula for surface area (attatched) will be relevant.

The Attempt at a Solution

Please see attached document for my workings and comments.

 

[HallsofIvy]

Many people will not open ".doc" files for fear of viruses. I happen to have pretty robust virus protection so I did. (I am "sneaking" a look at this at work. If I had been on my home computer I would not have.)

Two comments: You are using z²= x²+ y² or, in polar coordinates, z= r, as your cone. You were told that z is proportional to r and this cone has height h for r= R. What coefficient of proportion, k, do you need in z= kr so that when r= R, z=h?

Second, you get to $Area = (k)\int dA$ (I put in the "k") and then convert to polar coordinates to integrate. Why integrate at all? You know that $\int dA= A$, in other words, the area of the circular disk forming the bottom.

 

[irodus]

Thanks for your response! And sorry for attaching a .doc file however I have not worked out how to put equations into this text.

I have had some trouble in working out what k is, in z=kr. Firstly I let r=R as it should, then when z=h, k=R/h. I think there is a problem with my logic here. So I decided to compare kA with the answer I know I should get. This is what I got (sorry if it's messy):

pi(R)^2k=pi(R)(L) where L is sqrt(R^2+H^2) (the length of the side)
Rk=L
k=L/R
k=(sqrt(R^2+H^2))/R

So instead of having k=L/R, I have k=H/R. I am not sure how to come to this answer. Please explain where my reasoning has gone wrong here.

Your second point is very good, I should have realized that when I ended up with a pi(R)^2 in the answer. I suppose this means at least I got the bounds for my integral right?

Thankyou in advance for any help you provide!

 

[irodus]

bump

Any help here would be greatly appreciated! :)

 

[HallsofIvy]

"Bump"?? Gosh, I really apologize for not sitting right on the computer to be at your beck and call!

Now that I have that off my back, look at the cone "from the side" so that you have a triangle in the xz-plane. One way to do this is to recognize that the side of the cone is a line passing through (0,h) and (R,0). The equation of that line is a linear equation z= mx+ b. Since it goes through (0,h) we must have h= m(0)+ b so b= h. Since it goes through (R, 0), it we must have 0= m(R)+ b so m= -b/R. z= (-b/R)x+ b in the xz-plane. Because of the circular symmetry, as we rotate around the z-axis, "x" becomes the straight line distance from the z-axis: r in polar coordinates. z= (-b/R)r+ b or, perhaps more simply, z= b(1- r/R).

 

[irodus]

Sorry to bother you, but I don't think I understand your above post.

If z=b(1-r/R) we have:

z=kr
b(1-r/R)=kr
k=(b(1-r/R))/r

How do you get k=L/R from this?

Im not sure how this relates to the cone, as now we have introduced more variables. I thought R was just a way to describe r at a certain distance from the centre of the disc, D, underneath the cone.

Also, since the tip of the cone goes through the origin and is upside down, wouldn't the line z=mx+b always pass through (0,0), that is the z-intercept would be 0, making b=0 and the above substituion for z meaningless?

Thankyou in advance (and apologies for my rude post before, perhaps I should not use my internet slang all the time :P)

 

[HallsofIvy]

I went back and reread the original question. My derivation was assuming that the circular base was in the xy-plane and vertex at (0,0,h). In fact, the tip of the cone is at (0,0,0) and the base of the cone is in the plane z= h. Sorry about that.

This way, it's easier. Look at one side of the cone, in the y= 0 plane. that side is a line from (0,0,0) to (R,0,h). Since y is always 0 we can write that as z= mx+ b. Since z= 0 when x= 0, 0= m(0)+ b so b= 0. Since z= h when x= R, h= m(R) so m= h/R. That's your "k". z= (h/R)x. Again, rotating around the z-axis, that x becomes the more general "r". z= (h/R)r.

Or, as I said before, we can use 'similar triangles' (and, again, it is easier in this configuration). We have two similar right triangles, one, the whole cone, with vertices at (0, 0, 0), (R, h, 0), and (0,h,0). The smaller triangle, for general r, has vertices at (0,0,0), (0, z, 0) and (r, h, 0). For the larger triangle, the vertical side has length h and the horizontal side has length R. The ratio is h/R. For the smaller triangle, the corresponding sides are of length z and r and the ratio is z/r. Setting those equal, z/r= h/R so z= (h/R)r.

 

[irodus]

Thanks for the reply :)

That is clear to me now, I understand about the value for k. Unfortunately I still can't work out how to implement this into my working.

You said that Surface area=k*int(dA)

So when k=(H/R), and int(dA)=A (of disc underneath cone- as you said before), then Surface area=(H/R)*pi(R)^2 which is equal to pi(H)(R). This is similar to my first problem of getting k equal to (H/R) instead of (L/R), as I know formula for surface area of the cone to be equal to pi(R)(L).

Then I tried to calculate area being equal to (H/R) times the triple integral of r (dz r dr d(theta)) with bounds on theta of 0 to 2(pi) on r of 0 to R and on Z of 0 to H. I ended up with pi(R)(H)^2.

So I figured I was on the wrong track, and decided to do the triple integral (dz r dr d(theta)) with the bounds for theta being from 0 to 2(pi), r being from 0 to R and z being from 0 to (R/H)r. This would be so much easier to explain if I knew how to input equations! But I basically end up with the answer of:

Area=(2/3)pi(H)(R)^2 (which is starting to look similar to that of the volume of the cone).

I am having trouble connecting all of these answers I am coming up with! I know the solution is probably blatantly obvious, but I'm just having trouble seeing it.

Again, thankyou for taking the time to read over this, you've already been a huge help!

 

[irodus]

Am I thinking about this the wrong way?

 

[irodus]

Pleeeease can somebody help me on this, its driving me crazy!

I have inserted .jpg files of my working in the original post, hopefully nobody has a problem opening these!

Thanks heaps in advance guys, appreciate any help on this :)

 

[HallsofIvy]

I take the weekend off, okay?

Area=(2/3)pi(H)(R)^2 (which is starting to look similar to that of the volume of the cone).

But you don't want volume you want area. And the formula you give can't possibly be area, it has the wrong units. The formula for lateral surface area of a cone (not including the base) is $\pi r\sqrt{r^2+h^2}$.

Okay, we agree that z= (h/R)r. Looking at the cone from the side we see a right triangle with legs of length h and R so that the "lateral length", the hypotenuse of the triangle, is given by $\sqrt{R^2+ h^2}$. Similarly, a tiny piece, with dr instead of R and dz instead of h has "lateral length" $\sqrt{dr^2+ dz^2}= \sqrt{dr^2+ (h/R)^2dr^2}= \sqrt{1+ (h/R)^2}dr= \sqrt{h^2+ R^2}/R dr$. Rotating that around the z-axis gives a thin ribbon with that width and length the circumference of the circle: $2\pi r$. The area of that "ribbon" and the differential of area for the cone is the product of those:$2\pi\sqrt{h^2+ R^2}/R rdr$. To find the area of the cone, integrate that with respect to r. Of course, r goes from 0 to R.

A more advanced way to do this is to write the cone in parametric equations. Here, polar coordinates, r and $\theta$, work fine: $x= rcos(\theta)$, $y= rsin(\theta)$, z= (h/R)r. A "position vector" for a point on the cone is $/vec{r}= rcos(\theta)\vec{i}+ rsin(\theta)\vec{j}+ (h/R)r\vec{k}$. Differentiating with respect to r, we get $\vec{r}_r= cos(\theta)\vec{i}+ sin(\theta)\vec{j}+ (h/R)\vec{k}$. Differentiating with respect to $\theta$, we get $\vec{r}_\theta= -rsin(\theta)\vec{i}+ rcos(\theta)\vec{j}$. The "fundamental vector product" is the cross product of those vectors: $(h/R)rcos(\theta)\vec{i}-(h/R)rsin(\theta)\vec{j}+ r\vec{k}$. The differential area is given by the length of that vector:
$$\sqrt{(h/R)^2 r^2+ r^2}= \frac{\sqrt{h^2+ R^2}}{R}r$$
times $drd\theta$. That is, of course, just what we got before.

Finally, an elementary method- no calculus at all! Imagine cutting the cone in a straight line from its base to its vertex and flattening it. You can do that: through any point on a cone there exist a straight line through that point so it is a "developable surface"- any such surface can by "flattened" (unlike a sphere). We get a part of a circle. Not an entire circle because our circle has radius equal to the slant height of the cone: $\sqrt{R^2+ h^2}$ and circumference equal to the circuference of the base of the cone: $2\pi R$. The "portion" of the circle that we have is the ratio of that circumference to the circumference of a full circle of radius $\sqrt{R^2+ r^2}$: $(2\pi R)/(2\pi\sqrt{R^2+ h^2})= R/\sqrt{R^2+ h^2}$ and so the areas are in the same ratio. The area of an entire circle of radius $\sqrt{R^2+ h^2}$ would be $\pi(R^2+ h^2)$ so your cone has area $[R/\sqrt{R^2+ h^2}](\pi(R^2+ h^2))= \pi R\sqrt{R^2+ h^2}$ again.

 

[abu durgam]

thanks for ur help