HELP with thin film problem!!!

akmphy

1. The problem statement, all variables and given/known data

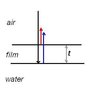
Consider a horizontal plane of thin film with
a thickness t. This film is located in between
air and water (see sketch). Light is directed
from the air downward through the film and
into the water, perpendicular to the surfaces.The index of refraction of the film n1 = 1.5.
The index of refraction of water is n2 = 1.33.
The wavelength of the incident wave in the air
is lambda air, and its frequency in air is f =
c/
.The wavelength lambda water of the light in the
water is:
and The smallest non-zero thickness t(min) leading
to no reflection is:

2. Relevant equations

t= m(lambda film)/2

3. The attempt at a solution
I know the net phase change equals one half of the wavelength because it undergoes a phase change from air to film, and experiences no phase change from film to water. I do not understand how to start this problem. I thought that the wave would reflect off the surface of the water, thus experiencing no wavelength in the water. Any help would be appreciated. No, I have no idea how to attach the image. It is three parallel surfaces, with n1 being the film, and n2 being the water

ehild

Only a little part of light reflects from water, the wast of it enters into the water, that is why you can see pebbles, fish and so on... Do you think it is total darkness below the surface of water????

ehild

akmphy

Logically, of course light enters the water. But, the diagrams insinuate that the ray is reflected off the surface of the water when going from gasoline's index of refraction, to water's index of refraction. For the problem set up..
a.)how would I even begin to calculate the smallest non zero thickness leading to no reflection?

t= m(lambda film)/2 which is destructive interference

b.)For algebraic representation of the wavelength of water, would it look like:

lamda water = n1/n2(lambda) ; this is one of the choices.

c.)Will the frequency of the light in the water decrease because the wavelength experiences destructive interference?

Thanks for any help.

akmphy

So far I understand that the frequency stays the same in the water, and that tmin= (lambda air)/2(n of film)
I still need help on the wavelength in the water in relation to the wavelength in the air:

(lambda air/ n of film)= lambda of film
lambda film/2 = lambda of water = [(lambda air/n of film)/2]/ n of water = lambda of water
This is not one of my choices.

ehild

The frequency (f) of the light is its inherent property, it does not change upon refraction.
Both the speed of propagation and the wavelength are different in different media.
The speed of light is v = c/n in a medium of refractive index n. The wavelength is λ=v/f, λ₀=c/f in vacuum. λ=λ₀/n.

The wave reflected from the air-film surface (red ray) interferes with the wave reflected from the film-water interface (blue ray). The interference is destructive if the phase difference of these waves is odd multiple of pi. The phase changes by pi upon reflection if the light enters into a higher index material from a lower index one.(So the phase of the blue ray differs by pi from the incident one.) In the opposite case, the phase does not change.
The phase of the wave changes by (2pi/λ)*x traversing a distance x in a medium. The blue ray in the picture traverses the thickness of the film twice. So its phase change is 2t*(2pi/λ). The phase difference between the blue and red rays is 4pi/λ-pi and it should be equal to pi(2m-1). (m is 1, 2 3 ...)

(4pi/ λ)t-pi=(2m-1)pi → (4pi/ λ)t=(2m)pi → 2t/λ=m*pi → t=mλ/2.

m=1 for the thinnest layer producing destructive interference, and

t=λ/2=λ₀/(2n_film).

You get minimum reflectance with that film, but not zero reflectance. Zero reflectance is obtained if the refractive index of the film is the geometric mean of those of the surrounding media. n_film=√(n_airn_substrate)

ehild

Attached Thumbnails

 

akmphy

Ehild,
I think I understand most of what you are saying.
As far as the wavelength of lambda water, are you saying that it is:

lambda water= Lambda air/ n of the water

That makes sense.

ehild

Yes, it is right.

ehild