Solve Pendulum Hitting Peg Problem with Conservation of Energy

[katyushak]

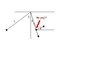
I have a problem that is driving me nuts. It involves a pendulum of length L pulled back an angle theta and released. After it goes through its lowest point, it encounters a peg alpha degrees out and r meters from the top of the string. The mass swings up about the peg until the string becomes slack with the mass falling inward and hitting the peg. I need to find theta through alpha, r, and L.

I guess the easiest way to go about it is through conservation of energy. I found the total energy of the system - it is all potential when pendulum is pulled back (mgh = mg Lcos (theta)), all kinetic at the lowest point, and mostly kinetic at the point alpha degrees off center where it hits the peg (mgLcos(theta) - mg(L-Lcos(alpha) = mv^2/(L-r)). I know the mass will swing certain distance (and a certain angle) past the horizontal axis before the string becomes "slack" and the mass pulls itself inward. I can't calculate the energy at this (highest) point. I know this is the last point where the mass is going in circular motion (radius L-r) that it began after hitting the peg and I know it is going off on projectile down towards the peg from that moment on.

I guess I need to know how it is that the string becomes "slack" - does the tension suddenly go away? Why would that be? Is the sum of forces acting on the body zero at this point so that the body no longer continues in a circle (acceleration not centripetal)? I can't quite put this condition in place. I think if I did, I'd be on the way to solving this. Or am I totally on the wrong track?

Thanks a lot for any hints.
katyushak

 

[ehild]

I guess I need to know how it is that the string becomes "slack" - does the tension suddenly go away? Why would that be? Is the sum of forces acting on the body is zero at this point so that the body no longer continues in a circle (acceleration not centripetal)? I can't quite put this condition in place. I think if I did, I'd be on the way to solving this. Or am I totally on the wrong track?

The tension "goes away", when the string becomes "slack" but not suddenly.
You know that a body needs a radial component of force - the centripetal force - so as it can move along a circle with speed v. Fcp= mv^2/R.
In your case, Fcp is the resultant of the tension in the string and the vertical component of gravity. Notice that a string can only pull, it cannot push an object. So the tension always points toward the centre of the circle.

If it happens that the speed of the body that you got from energy conservation drops to a value vo, so as Fcp equals to the radial component of gravity, no tension would be needed to keep the body along the circle with that speed. But the speed decreases further as the body moves upward, and then the pull of gravity is higher than should be to move along the circle with the former radius, so the body moves inward. It would remain in orbit only if it had be pushed by the string, but this is impossible. The string does not act on the body any more as it reaches the critical speed vo. That means the body moves under the influence of gravity alone from there on, it moves like a projectile.

 

[katyushak]

The string does not act on the body any more as it reaches the critical speed vo. That means the body moves under the influence of gravity alone from there on, it moves like a projectile.

Would that mean that at the critical, highest point, the speed of the body would be magnitude v = sqrt (FR/m) which is same v that the body had when the body began its circular motion and direction perpendicular to the radius - meaning that when the body starts its projectile motion, it has a starting velocity that is the same magnitude as when it just started moving along a circle?

Seems like I am wrong here about velocity because if it were the same, then this body would have both potential and kinetic energy, where its potential energy would depend on the height it went to and its kinetic energy would be the same as in point where it hit the peg (bottom of the circular trajectory) - meaning I don't have conservation of energy (potential energy increased due to height but kinetic did not change due to same v)! Please help...

 

[ehild]

Would that mean that at the critical, highest point, the speed of the body would be magnitude v = sqrt (FR/m)

No. Why should it be?

ehild

 

[katyushak]

Thanks ehild for your reply. I see now that the velocity is not constant since acceleration is not constant - because acceleration is a function of the sum of all forces (sorta) and the forces change. Thus, I have two questions that I think if I get answered will help me solve this completely:

1. I need to find the velocity of the body at the point where tension is zero. Say, at this point the body is beta degrees above a horizontal ("horizontal" being perpendicular to the "vertical" - where the original pendulum is at its lowest point). At this point, tension T = 0 so ma * cos(beta) =mg or
mv^2*cos(beta)/R = mg - right? Problem is, this does not help me find v since I don't know beta! Could you help?

2. If I got help on question 1 and found this velocity, I would be able to find its kinetic energy and thus its potential energy (because I know the total energy of the system and I ignore the work done by other forces on the body - like friction/air/etc). But since velocity is a vector, what direction do I use to calculate kinetic energy? Just the magnitude I would assume since kinetic energy is a scalar but I wanted to double-check.

Once I know this v at the point the mass hits the peg, I can plug it into the equation for my energy at this point.

Looking forward to any clues.

Thanks a lot for checking this out!
katyushak

 

[ehild]

T
1. I need to find the velocity of the body at the point where tension is zero. Say, at this point the body is beta degrees above a horizontal ("horizontal" being perpendicular to the "vertical" - where the original pendulum is at its lowest point). At this point, tension T = 0 so ma * cos(beta) =mg or
mv^2*cos(beta)/R = mg - right? Problem is, this does not help me find v since I don't know beta! Could you help?

See the free-body diagram: The forces acting on the body of the pendulum are gravity and tension, but we want to find the position when the tension is zero.
Force is a vector and so does acceleration. They have two components in the plane of the motion, and usually we decompose them into radial and tangential components. The radial component of G is m*g*sin(beta). The total radial force is in general $$F_r=m*g*\sin(\beta) + T$$ and this should be equal to the centripetal force $$mv^2/R$$.

In your case T=0 and the radius is l so

$$mv^2/l = mg\sin (\beta)$$

This is one equation with two unknowns, beta and v. But you can write an other equation for the energy. Try.

 

[koa]

i`m also working on this problem, and here`s what i end up with
the intial potential energy= mg(L-Lcos(theta))
final energy will equal the sumtion of kinetic energy and potential= mg(l-rcos(alfa)) + .5mgv^2
i still don`t know how to get the velocity?

i got one equation in twon unknowns??
mg sin(beta)=.5mv^2/(l-R)
but i still don`t get the energy equation ??

 

[ehild]

i`m also working on this problem,

Koa,

What is the problem exactly? Should the body fall on the peg and the starting angle is the question when this happens? Or you have to find the angle above the horizontal when the string gets "slack"?

ehild

 

[katyushak]

ehild,

The problem is to find the relationship between the angles and radius/string, i.e., find theta. Here is the answer, I just don't quite know how to get there:

cos (theta) = (R/L)cost (alpha) - [sqrt(3)/2][1-R/L]

katyushak

 

[ehild]

ehild,

The problem is to find the relationship between the angles and radius/string, i.e., find theta. Here is the answer, I just don't quite know how to get there:

cos (theta) = (R/L)cost (alpha) - [sqrt(3)/2][1-R/L]

katyushak

All right, both you and Koa started to solve the problem correctly, with conservation of energy. If we assume that the string makes an angle beta with the horizontal at the end when it becomes "slack", the height h2 of the body is here

$$h_2=L-R\cos{\alpha}+(L-R)\sin{\beta}$$

From conservation of energy:
$$mgh_0=mgh_2+\frac{ mv^2}{2}$$

The string becomes slack when

$$\frac{mv^2}{R-L}=mg\sin{\beta} \rightarrow v^2=g(R-L)\sin{\beta}$$

Inserting v^2 into the equation for energy, and solving for sin(beta), we get

$$\sin{\beta}=\frac{2}{3}*\frac{R\cos{\alpha}-L\cos{\theta}}{L-R}$$

Using this expression, v^2 becomes

$$v^2=\frac{2g}{3}*(R\cos{\alpha}-L\cos{\theta})$$

From here, we have a projectile motion with initial velocity of magnitude vo=v and an angle of beta with the vertical. The motion ends at the peg, at a displacement

$$x =(L-R)\cos{\beta} = v_{0x}t=(v_0\sin{\beta})*t$$

$$y= -(L-R)\sin{\beta}=v_{0y}t-\frac{g}{2}t^2=(v_0\cos{\beta})*t-\frac{g}{2}t^2$$
Eliminate the time, use the expressions for v0 and sin(beta) and the result hopefully is
$$\cos{\theta}=\frac{R}{L}*\cos{\alpha}-\frac{\sqrt{3}}{2}(1-R/L)$$

Check my derivation, I might have made mistakes in typing.

ehild

 

[katyushak]

Hi,

Thanks for the step-by-step. I've been working through these very formulas for two weeks now (ever since you helped me solve the confusion about how the string becomes slack) but just could not get the right answer: I am still not getting your expression for sin (beta) but I think this is a trigonometry/arithmetics problem at this point. I'll trace your steps and try to find out where I was wrong.

Thanks a lot for your help and time, it's been very beneficial, especially the hints and explanations!

katyushak

 

[katyushak]

Math doesn't work out

ehild,

It looks like the math does not work out to be what it is supposed to be.

I was able to get your expression for sin (beta) and it looks like v^2 should be 2g/3(Lcos[theta] - R cos [alpha] (the opposite of your expression, if I am not mistaken). Either way, I end up with the following for cos (theta):

cos [theta] = (R/L)cos (a) + 3(L-R)cos^2(beta)/2Lsin(beta)

which can't be simplified much beyond this form, it seems, other than to get rid of cos^2(beta) as in cos^2(beta) = 1 - sin^2(beta). So, unless I consistently make mistakes in my arithmetics, we must be missing some important condition to solve this problem.

Any advice would be appreciated. Thanks!

katyushak

 

[ehild]

Either way, I end up with the following for cos (theta):

cos [theta] = (R/L)cos (a) + 3(L-R)cos^2(beta)/2Lsin(beta)

which can't be simplified much beyond this form, it seems, other than to get rid of cos^2(beta) as in cos^2(beta) = 1 - sin^2(beta).

katyushak

Do it, and than replace sin(beta) with the formula you got for it,
and simplify.

I will check my writing again, I might have done some mistakes when typing in. I used an other arrangement, so there can be some confusion in my signs.

ehild

 

[katyushak]

Quite a long equation

Ok, I get this scary thing that I can't simplify (left side has all cos(theta)'s and right side has the rest):

4LR cos^2(alpha)cos(theta) - 8Lcos(alpha)cos^2(theta) + 8Rcost(theta) - *L^2Rcost(alpha)cost(theta) - 4L^3cost(alpha)cos^2(theta) = 4L^2cost(alpha) +9L^3cost(alpha - 18L^2Rcos(alpha) + 9LR^2cos(alpha) - 4LRcos^3(alpha)

! Am I missing some simplification I could have done before I got here?... Is there a computer problem that can solve this for me or something?...

Thanks for all your time on this ehild. It turns out to be more of a math nightmare than a physics problem. This is supposed to be for a physics class, not arithemetics marathon...

 

[ehild]

ehild,

It looks like the math does not work out to be what it is supposed to be.

I was able to get your expression for sin (beta) and it looks like v^2 should be 2g/3(Lcos[theta] - R cos [alpha] (the opposite of your expression, if I am not mistaken).

Yes, it was a typo in v^2.

From the condition of "slack":

$$v^2=g(L-R)\sin{\beta}$$

Inserting into the equation fro conservation of energy:

$$v^2=\frac{2g}{3}(R\cos{\alpha}-L\cos{\theta})$$

Back to "slack":

*$$\sin{\beta}=\frac{2}{3}\frac{R\cos{\alpha}-L\cos{\theta}}{L-R}$$

I think it is easier to proceed by introducing the notation

$$R\cos{\alpha}-L\cos{\theta}=B$$

Then

$$v^2=\frac{2gB}{3}$$

*$$\sin{\beta}=\frac{2B}{3(L-R)}$$

Either way, I end up with the following for cos (theta):

cos [theta] = (R/L)cos (a) + 3(L-R)cos^2(beta)/2Lsin(beta)

I got

$$\frac{R}{L}\cos{\alpha}-\frac{3(L-R)\cos^2{\beta}}{4\sin{\beta}}$$

But it is easier to keep

$$R\cos{\alpha}-L\cos{\theta}=B$$

unresolved.

I got for the projectile part:

$$3(L-R)\cos^2{\beta}=4B\sin{\beta}$$

Replacing * for sin(beta)

$$3(L-R)(1-(\frac{2B}{3(L-R)})^2)=4B\frac{2B}{3(L-R)}$$

$$3(L-R)-\frac{4B^2}{3(L-R)}=\frac{8B^2}{3(L-R)}$$

$$\frac{12B^2}{3(L-R)}=3(L-R)$$

$$4B^2=3(L-R)^2$$

$$B=\sqrt{3}/2(L-R)$$

and you get theta from here...But you are right, this was an arithmetics marathon. .

ehild

 

[katyushak]

Wow, your derivation is a thing of beauty! I see that I need to ramp up on doing such long algebraic equations - I saw that Rcos (alpha) - L cost (theta) was being repeated a few times and tried to keep it "as is" but did not quite go the extra step of doing the substitutions. This makes it all so clean!

Thanks a lot for your help again, ehild! I think this little exercise has been very helpful for me.

katyushak

 

[ehild]

Wow, your derivation is a thing of beauty!
katyushak

I am really happy that you have found beauty in a long and nasty derivation :rofl: . I was surprised on the simplicity of the formula at the end, and I just guess that there might have been a simpler way to get it. Anyway, that was a genuine international research project of ours and I enjoyed it quite much.

ehild