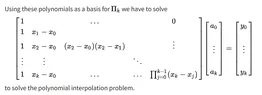anuttarasammyak's latest activity
-
 anuttarasammyak reacted to Kostik's post in the thread A Dirac's integral for the energy-momentum of the gravitational field with
anuttarasammyak reacted to Kostik's post in the thread A Dirac's integral for the energy-momentum of the gravitational field with Like.
@anuttarasammyak Excellent! This was hugely helpful. I wish Dirac had been a little less cryptic. It's not often that one consults...
Like.
@anuttarasammyak Excellent! This was hugely helpful. I wish Dirac had been a little less cryptic. It's not often that one consults... -
 anuttarasammyak reacted to Kostik's post in the thread A Dirac's integral for the energy-momentum of the gravitational field with
anuttarasammyak reacted to Kostik's post in the thread A Dirac's integral for the energy-momentum of the gravitational field with Like.
@anuttarasammyak Very helpful, thanks. I should have looked there, because Dirac's book takes a lot from LL. In my copy of LL, this...
Like.
@anuttarasammyak Very helpful, thanks. I should have looked there, because Dirac's book takes a lot from LL. In my copy of LL, this... -
 anuttarasammyak replied to the thread A Dirac's integral for the energy-momentum of the gravitational field.@Kostic As for your question the explanation of L-L : seems a good complementary to Dirac.
anuttarasammyak replied to the thread A Dirac's integral for the energy-momentum of the gravitational field.@Kostic As for your question the explanation of L-L : seems a good complementary to Dirac. -
 anuttarasammyak replied to the thread Other Considering the change from CMP to AMO.I do not have academic background but I am involved in management of quantum computing research in a public institute. I observe most...
anuttarasammyak replied to the thread Other Considering the change from CMP to AMO.I do not have academic background but I am involved in management of quantum computing research in a public institute. I observe most... -
 anuttarasammyak replied to the thread B Average velocity as a weighted mean.Thanks @Ibix So in other words $$ \frac{1}{\bar{v}}=\sum_i \frac{r_i}{v_i} $$ where r_i is ratio of i-th segment's length to the whole...
anuttarasammyak replied to the thread B Average velocity as a weighted mean.Thanks @Ibix So in other words $$ \frac{1}{\bar{v}}=\sum_i \frac{r_i}{v_i} $$ where r_i is ratio of i-th segment's length to the whole... -
 anuttarasammyak reacted to Ibix's post in the thread B Average velocity as a weighted mean with
anuttarasammyak reacted to Ibix's post in the thread B Average velocity as a weighted mean with Like.
The parallel resistors formula comes from the continuity equation relating the input current ##I## to the currents ##I_i## through the...
Like.
The parallel resistors formula comes from the continuity equation relating the input current ##I## to the currents ##I_i## through the... -
 anuttarasammyak replied to the thread B Average velocity as a weighted mean.Your "arismetic mean of inverse" in reminds me of law of synthesizede resistance of parallel ressitors $$...
anuttarasammyak replied to the thread B Average velocity as a weighted mean.Your "arismetic mean of inverse" in reminds me of law of synthesizede resistance of parallel ressitors $$... -
 anuttarasammyak replied to the thread B Average velocity as a weighted mean.Just for a fun I observe $$ \bar{v}=\frac{\sqrt{v_1v_2}}{\frac{v_1+v_2}{2}}\sqrt{v_1v_2} \leq \sqrt{v_1v_2} $$
anuttarasammyak replied to the thread B Average velocity as a weighted mean.Just for a fun I observe $$ \bar{v}=\frac{\sqrt{v_1v_2}}{\frac{v_1+v_2}{2}}\sqrt{v_1v_2} \leq \sqrt{v_1v_2} $$ -
 anuttarasammyak replied to the thread B Average velocity as a weighted mean.$$\bar{v}=\frac{2L}{L/v_1+L/v_2}=\frac{2v_1v_2}{v_1+v_2}$$ I am not sure what are harmonic mean and weighted average you say in this result.
anuttarasammyak replied to the thread B Average velocity as a weighted mean.$$\bar{v}=\frac{2L}{L/v_1+L/v_2}=\frac{2v_1v_2}{v_1+v_2}$$ I am not sure what are harmonic mean and weighted average you say in this result. -
 anuttarasammyak replied to the thread Family of lines that are at a distance of 5 from the origin.$$y-5\sin\omega=-\frac{1}{\tan\omega}(x-5\cos\omega)$$ [EDIT] Another way. Say all the points on the line $$ y=ax+b $$ has distance...
anuttarasammyak replied to the thread Family of lines that are at a distance of 5 from the origin.$$y-5\sin\omega=-\frac{1}{\tan\omega}(x-5\cos\omega)$$ [EDIT] Another way. Say all the points on the line $$ y=ax+b $$ has distance... -
 anuttarasammyak replied to the thread Family of lines that are at a distance of 5 from the origin.The nearest point of the lines are on the circle x^2+y^2=5^2. The lines are orthogonal to the circle radius.
anuttarasammyak replied to the thread Family of lines that are at a distance of 5 from the origin.The nearest point of the lines are on the circle x^2+y^2=5^2. The lines are orthogonal to the circle radius. -
 anuttarasammyak replied to the thread I Why work is PdV and not (P+dP)dV in an isothermal process?.dP dV is infinitesimal of second order. We can disregard it in calculation.
anuttarasammyak replied to the thread I Why work is PdV and not (P+dP)dV in an isothermal process?.dP dV is infinitesimal of second order. We can disregard it in calculation. -
 anuttarasammyak replied to the thread I Useless continued fraction for 1.Generalizing 2 to integer n, the equation is $$x^2-nx+1=0$$ $$x=\frac{n \pm \sqrt{n^2-4}}{2}$$ So we know for x to exist ##|n|\geq 2##...
anuttarasammyak replied to the thread I Useless continued fraction for 1.Generalizing 2 to integer n, the equation is $$x^2-nx+1=0$$ $$x=\frac{n \pm \sqrt{n^2-4}}{2}$$ So we know for x to exist ##|n|\geq 2##... -
 anuttarasammyak replied to the thread I Useless continued fraction for 1.Say RHS continued fraction is x, we have an equation $$x=2-\frac{1}{x}$$ $$(x-1)^2=0$$ $$x=1$$ So we know if x converges, x=1. If it...
anuttarasammyak replied to the thread I Useless continued fraction for 1.Say RHS continued fraction is x, we have an equation $$x=2-\frac{1}{x}$$ $$(x-1)^2=0$$ $$x=1$$ So we know if x converges, x=1. If it... -
 anuttarasammyak replied to the thread I Proving Newton's forward difference interpolation formula.https://en.wikipedia.org/wiki/Newton_polynomial shows : The matrix is downer triangular matrix. Solving it from the top law and...
anuttarasammyak replied to the thread I Proving Newton's forward difference interpolation formula.https://en.wikipedia.org/wiki/Newton_polynomial shows : The matrix is downer triangular matrix. Solving it from the top law and...