bob012345's latest activity
-
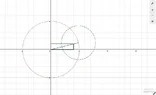
 bob012345 replied to the thread High School Three Squares Problem.Expanding the original problem to be an ## nx1## rectangle, it turns out the angle B to add to angle A (defined by the ratio...
bob012345 replied to the thread High School Three Squares Problem.Expanding the original problem to be an ## nx1## rectangle, it turns out the angle B to add to angle A (defined by the ratio... -
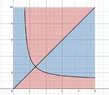
 bob012345 replied to the thread Undergrad Comparing ##a^b## and ##b^a##.One can take the log of both side of the inequality and plot that. That plot looks identical but goes on exponentially further. The...
bob012345 replied to the thread Undergrad Comparing ##a^b## and ##b^a##.One can take the log of both side of the inequality and plot that. That plot looks identical but goes on exponentially further. The... -
 bob012345 reacted to AlexB23's post in the thread Undergrad Comparing ##a^b## and ##b^a## with
bob012345 reacted to AlexB23's post in the thread Undergrad Comparing ##a^b## and ##b^a## with Like.
Demos is the greatest of all time calculator. Used it a bit in high school over a decade ago, and it helped me visualize math concepts.
Like.
Demos is the greatest of all time calculator. Used it a bit in high school over a decade ago, and it helped me visualize math concepts. -
 bob012345 replied to the thread Undergrad Comparing ##a^b## and ##b^a##.The plot can also be generated easily on Desmos.
bob012345 replied to the thread Undergrad Comparing ##a^b## and ##b^a##.The plot can also be generated easily on Desmos. -
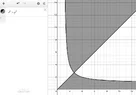
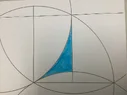
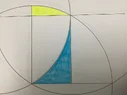
 bob012345 replied to the thread Undergrad Three Circle Problem.It can be shown that the yellow figure of the last graphic in post #8 can be completely contained in the blue figure. Take off an...
bob012345 replied to the thread Undergrad Three Circle Problem.It can be shown that the yellow figure of the last graphic in post #8 can be completely contained in the blue figure. Take off an... -
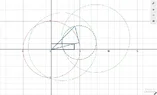
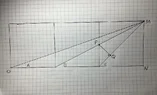
 bob012345 replied to the thread High School Three Squares Problem.Here is another way but it’s just a variation of @coquelicot above in post #7 but the lengths are not obvious so they must be...
bob012345 replied to the thread High School Three Squares Problem.Here is another way but it’s just a variation of @coquelicot above in post #7 but the lengths are not obvious so they must be... -
 bob012345 reacted to Steve4Physics's post in the thread High School Three Squares Problem with
bob012345 reacted to Steve4Physics's post in the thread High School Three Squares Problem with Like.
The solution below is not mine – I saw it on YouTube, here. This is just my summary. 1. Add 3 squares and consider the triangle...
Like.
The solution below is not mine – I saw it on YouTube, here. This is just my summary. 1. Add 3 squares and consider the triangle...