bob012345's latest activity
-
 bob012345 replied to the thread Undergrad Find the Number of Triangles.Ok. You can figure the upper bound of total possible triangles and go down from there.
bob012345 replied to the thread Undergrad Find the Number of Triangles.Ok. You can figure the upper bound of total possible triangles and go down from there. -
 bob012345 reacted to FactChecker's post in the thread Undergrad Find the Number of Triangles with
bob012345 reacted to FactChecker's post in the thread Undergrad Find the Number of Triangles with Like.
I would consider that to be automating a "brute force counting" method. IMO, although it is not what the OP asked for, it is still an...
Like.
I would consider that to be automating a "brute force counting" method. IMO, although it is not what the OP asked for, it is still an... -
 bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with
bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with Like.
The formula for the 2nd and the 3rd case is written as $$\frac{a^2+s^2-as(\sin\theta + \cos\theta)}{2 \sin\theta \cos\theta}$$ which is...
Like.
The formula for the 2nd and the 3rd case is written as $$\frac{a^2+s^2-as(\sin\theta + \cos\theta)}{2 \sin\theta \cos\theta}$$ which is... -
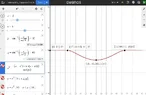
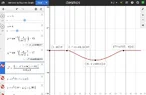
 bob012345 replied to the thread High School Area of Overlapping Squares.Interesting observation! It appears so if both values are within the range of the functions. Looking at ##(a,s)## being (4,5) vs...
bob012345 replied to the thread High School Area of Overlapping Squares.Interesting observation! It appears so if both values are within the range of the functions. Looking at ##(a,s)## being (4,5) vs... -
 bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with
bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with Like.
The answers for the first case and the 4th case are symmetric for exchange of s and a. May we expect the same for the 2nd and the 3rd...
Like.
The answers for the first case and the 4th case are symmetric for exchange of s and a. May we expect the same for the 2nd and the 3rd... -
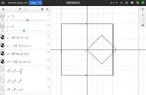
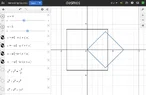
 bob012345 replied to the thread High School Area of Overlapping Squares.I worked out the overlap of the two squares as a function of angle. Given ##a## is the half edge length of the original square and...
bob012345 replied to the thread High School Area of Overlapping Squares.I worked out the overlap of the two squares as a function of angle. Given ##a## is the half edge length of the original square and... -
 bob012345 replied to the thread High School Area of Overlapping Squares.Agreed. Now the larger square is the 1m square. The overlap depends on the relative orientation until ##s## shrinks to...
bob012345 replied to the thread High School Area of Overlapping Squares.Agreed. Now the larger square is the 1m square. The overlap depends on the relative orientation until ##s## shrinks to... -
 bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with
bob012345 reacted to anuttarasammyak's post in the thread High School Area of Overlapping Squares with Like.
$$s=\sqrt{2}/2$$is the minimum value satisfying it though not larger any more. And also $$s=\frac{1}{2\sqrt{2}} $$is the maximum.
Like.
$$s=\sqrt{2}/2$$is the minimum value satisfying it though not larger any more. And also $$s=\frac{1}{2\sqrt{2}} $$is the maximum. -
 bob012345 replied to the thread High School Area of Overlapping Squares.The next level is if we let the length ##s## of the larger square vary, what range of values of ##s## will your statement not be true?
bob012345 replied to the thread High School Area of Overlapping Squares.The next level is if we let the length ##s## of the larger square vary, what range of values of ##s## will your statement not be true?