Recent content by surfwavesfreak
-
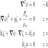
Graduate What are the boundary conditions for rotational flow?
Yes you are right. Following what you said, may be a very straightforward boundary condition would be : ∇p×∇ζ=0, z=ζ as the pressure is constant along the surface, its gradient should always be directed ortohogonally to the surface of the fluid. Then you get an equation that you can easily cast...- surfwavesfreak
- Post #7
- Forum: Mechanics
-
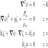
Graduate What are the boundary conditions for rotational flow?
I was thinking that may be you could cast p=0, z=ζ and the navier stokes equations : ∂tui+uj∂xjui=-∂xip/ρ+gδiz which I assumed to be valid everywhere, especially at z=ζ As p=0, ∂xip=0 as well, and you are left with : ∂tui+uj∂xjui=gδiz, z=ζ but I've never seen that anywhere, and I think there may...- surfwavesfreak
- Post #5
- Forum: Mechanics
-
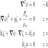
Graduate What are the boundary conditions for rotational flow?
Thanks for your link, but I did not see any equation like ∂tφ+½(∇φ)2+gζ=0, z=ζ where the pressure is actually removed from the variables. Any idea ?- surfwavesfreak
- Post #3
- Forum: Mechanics
-
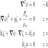
Graduate What are the boundary conditions for rotational flow?
Hello everyone, The boundary condition : P=0, z=ζ is very common when studying irrotational flows. When cast with the Bernoulli equation, it gives rise to the famous dynamic boundary conditionn, which is much more convenient : ∂tφ+½(∇φ)2+gζ=0, z=ζ But what happens if the motion is rotational ...- surfwavesfreak
- Thread
- Bernoulli equation Boundary Boundary condition Condition Fluid mechanics Ocean wave
- Replies: 7
- Forum: Mechanics
-
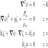
Bonjour - french physical PhD student
Hello every body, I am very excited to be now part of your community. Me in a few words : I am french PhD student, working in the field of physical oceanography for 2 years now., more specifically on the wonderful topic of ocean surface waves. I am particularly interested in asking you some...- surfwavesfreak
- Thread
- fluid mechanics oceanography phd
- Replies: 1
- Forum: New Member Introductions