- #1
teodron
- 7
- 0
Hello,
First of all, please excuse me if I posted in the inappropriate place.. While a student few years ago, I used to work a lot with advanced differential geometry concepts, but never got an intuitive view of HOW humanity got to think about parallel transport, why it contained two words that describe an action and a condition and why these words, in reality, do not suffice to carry out this process.
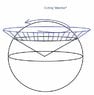
Coming back to this issue, I always started with a sphere. I used to move a cigar along an orange, while trying to keep it tangent to a latitude circle. If that was not the equator, I was supposed to get a different position for that vector/cigar when I came back and crossed the start point. It didn't quite happen, so I didn't understand HOW to carry that cigar along the surface of the orange while that same latitude circle and not end up with the same orientation for the cigar.
I asked my Diff Geom TA to explain the concept to me, apart from the covariant derivative definition and other unintuitive devices.. He didn't shed any light on the issue. Now I'm at work and can't find peace of mind. I think of this concept in two ways, both of which can be dangerously incorrect:
1. Parallel transport means: move with a particle across a surface, along a predescribed path. You want to keep on track, thus you must shift your velocity vector. If you can do that without pushing or lifting from the surface (no normal velocity), then the path is a geodesic. If the path is a geodesic, then the velocity vector should be parallel to itself at any point on that path embedded in the surface. Now, if you view that vector from the outside space (sphere to 3d space analogy, the vector is in no way parallel to whatever it was looking like at the past instances). Then I think and say to myself: the parallel concept must be related to how the normal looks like and how the tangent space looks like, and thus how they change.. Maybe I'm on the right track: anywhere on the sphere, I know the "up" direction and the "left" direction.. they can be given by the way the sphere/surface is parametrized, right? I think Gauss said something important about this aspect, but I'm interested in analyzing the problem from above, so I need the normal and left vectors.. If I move a bit forward, I have to take a tiny turn to stay on the parallel circle/latitude circle. The turning amount is a vector in the tangent space in that point to the sphere. Then by this same transformation I have to "shift" the cigar/the vector I'm trying to parallel transport. This can be a rotation about the UP/normal vector, that is given by the surface's geometry. Now I end up with another vector that is not parallel, of course, to its previous counterpart. Or is it? I can see that if I reach the start point by encircling the sphere in such a manner, I might end up with a vector pointing in a different direction, thus, being back to the same tangent plane, and having the vectors in this plane, they are not parallel, hence the latitude circles are not geodesics (apart from equators). What I can't understand is why the velocity vector of this latitude circle isn't parallel to itself. It just doesn't add up.. when I return to the start point, it has to point in the same direction, right?
2. Smaller explanation following: a surface, an embedded curve/path/trajectory, a vector field/vector that is parallel transported along the curve. The result? some kind of a ribbon given by the point c(t) on the curve and another point d(t) given by the endpoint of the X(c(t)) tangent vector.. Now the resulting swept/pseudo swept surface is a ribbon like object, at least for a sphere. If that were to be a ribbon resulting from the movement across a geodesic, then this ribbon should have no torsion? Or, at least, the measure that gives the intuitive torsion factor for a curve (torsion free curves are planar, right?) should tell something about that curve as to how close to being a geodesic it actually is. Given such a ribbon, I used to imagine two infinitely close line segments or lines, like the planes of a capacitor (the electrical symbol) and if I try to insert that ribbon through this vent, I will not be able to do it unless it comes from a paralle transport process..
These were the two questions I asked my TA. he couldn't answer, and I'm sincerely haunted by this years old question.. I feel like my life has no meaning, I can't rest not being able to understand this rather essential concept. So, I kindly ask of you to help me out. I should state that I've did a bit of forum research and the subject I've found don't help that much. I don't want to go back to Christoffel symbols, covariant and contravariant fields, tensor derivatives, etc.. I first want to understand how the human mind stumbled upon this concept, then I will be glad to understand how to generalize it.
Best wishes!
Theodore
First of all, please excuse me if I posted in the inappropriate place.. While a student few years ago, I used to work a lot with advanced differential geometry concepts, but never got an intuitive view of HOW humanity got to think about parallel transport, why it contained two words that describe an action and a condition and why these words, in reality, do not suffice to carry out this process.
Coming back to this issue, I always started with a sphere. I used to move a cigar along an orange, while trying to keep it tangent to a latitude circle. If that was not the equator, I was supposed to get a different position for that vector/cigar when I came back and crossed the start point. It didn't quite happen, so I didn't understand HOW to carry that cigar along the surface of the orange while that same latitude circle and not end up with the same orientation for the cigar.
I asked my Diff Geom TA to explain the concept to me, apart from the covariant derivative definition and other unintuitive devices.. He didn't shed any light on the issue. Now I'm at work and can't find peace of mind. I think of this concept in two ways, both of which can be dangerously incorrect:
1. Parallel transport means: move with a particle across a surface, along a predescribed path. You want to keep on track, thus you must shift your velocity vector. If you can do that without pushing or lifting from the surface (no normal velocity), then the path is a geodesic. If the path is a geodesic, then the velocity vector should be parallel to itself at any point on that path embedded in the surface. Now, if you view that vector from the outside space (sphere to 3d space analogy, the vector is in no way parallel to whatever it was looking like at the past instances). Then I think and say to myself: the parallel concept must be related to how the normal looks like and how the tangent space looks like, and thus how they change.. Maybe I'm on the right track: anywhere on the sphere, I know the "up" direction and the "left" direction.. they can be given by the way the sphere/surface is parametrized, right? I think Gauss said something important about this aspect, but I'm interested in analyzing the problem from above, so I need the normal and left vectors.. If I move a bit forward, I have to take a tiny turn to stay on the parallel circle/latitude circle. The turning amount is a vector in the tangent space in that point to the sphere. Then by this same transformation I have to "shift" the cigar/the vector I'm trying to parallel transport. This can be a rotation about the UP/normal vector, that is given by the surface's geometry. Now I end up with another vector that is not parallel, of course, to its previous counterpart. Or is it? I can see that if I reach the start point by encircling the sphere in such a manner, I might end up with a vector pointing in a different direction, thus, being back to the same tangent plane, and having the vectors in this plane, they are not parallel, hence the latitude circles are not geodesics (apart from equators). What I can't understand is why the velocity vector of this latitude circle isn't parallel to itself. It just doesn't add up.. when I return to the start point, it has to point in the same direction, right?
2. Smaller explanation following: a surface, an embedded curve/path/trajectory, a vector field/vector that is parallel transported along the curve. The result? some kind of a ribbon given by the point c(t) on the curve and another point d(t) given by the endpoint of the X(c(t)) tangent vector.. Now the resulting swept/pseudo swept surface is a ribbon like object, at least for a sphere. If that were to be a ribbon resulting from the movement across a geodesic, then this ribbon should have no torsion? Or, at least, the measure that gives the intuitive torsion factor for a curve (torsion free curves are planar, right?) should tell something about that curve as to how close to being a geodesic it actually is. Given such a ribbon, I used to imagine two infinitely close line segments or lines, like the planes of a capacitor (the electrical symbol) and if I try to insert that ribbon through this vent, I will not be able to do it unless it comes from a paralle transport process..
These were the two questions I asked my TA. he couldn't answer, and I'm sincerely haunted by this years old question.. I feel like my life has no meaning, I can't rest not being able to understand this rather essential concept. So, I kindly ask of you to help me out. I should state that I've did a bit of forum research and the subject I've found don't help that much. I don't want to go back to Christoffel symbols, covariant and contravariant fields, tensor derivatives, etc.. I first want to understand how the human mind stumbled upon this concept, then I will be glad to understand how to generalize it.
Best wishes!
Theodore