Time taken for pressure to equalise?

[serverxeon]

I have a hemisphere dome, which volume = $\frac{2}{3}$∏r³
Inside the dome, pressure is 1atm (assume 1.05 kPa)
Outside the dome, pressure is 0.01atm (10.5 Pa)
I then puncture a 0.2 cm² (2 x 10^-5 m²) hole on the flat side of the dome.

Question: Find time taken for pressure to equalise.

--------------

I have searched up the internet, and seems that I have to use bernoulli. But I have a few problems.

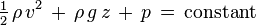
1) I have no idea what to substitute for the variables.
2) Are the density of air inside and outside the dome different?
3) How should I use calculus (or differential equations, or anything else) to find the time taken, given the process is non-linear in relation.

Thanks

 

[Hobold]

I don't think you can use Bernoulli's equation to solve, as most requirements are not met (dm/dt is not constant, air is not incompressible. You may use its differential form, though:

$$\frac{dp}{\rho} + d(\frac{v^2}{2}) + g dz = 0$$

Now you'll have to make a few hypothesis, such as the processes is not turbulent (which it is, however, though it would be almost impossible to accurately describe this phenomenon without this consideration, so your answer will be physically wrong), the air is an ideal gas (or find a good equation of state, though ideal gas law is good).

The specific mass of air in both situations are different, but remember that they must equal when in equilibrium.

The differential equation you will have to solve will be a combination of that differential form of Bernoulli's law and the fact that

$$\frac{dm}{dt} = V \frac{d\rho}{dt} = Av$$

Interesting problem, by the way.

 

[serverxeon]

Thanks for the reply,

But I'll like to clarify, how is rate of change of mass = area * velocity?

$$\frac{dm}{dt} = V \frac{d\rho}{dt} = Av$$

 

[Hobold]

I'm sorry, that's wrong of course, must've been my distraction. It should be

$$\frac{dm}{dt} = V\frac{d\rho}{dt} = \rho A v$$

 

[serverxeon]

thanks pal,

but I am looking at the equations, and am thinking...
Pressure will change as the process equalise, and density will change as pressure change, so mass in the dome will change too. At the same time velocity changes too... So I have multiple interrelated quantities.. and er...

Can someone please guide me on how should I start?
I'm like just stuck!

 

[Hobold]

Yes, everything changes and that's why you use a differential equation to solve this problem.

You will have to work with three equations:

1) Differential form of Bernoulli's
2) Rate of change of mass
3) Ideal gas law

Can you find a equation for velocity using 1) and 3)? Tip: make a few assumptions, one of them is to ignore gravity effects (the dome is too small).