- #1
einfall
- 11
- 0
Snell's Law - complex angle of refraction (need "complement")
I'm tying myself in knots trying to calculate something I think should be very simple. I'm writing/debugging some code at the moment, and I simply don't know if this silly problem is the source of the major errors I'm currently seeing. Some help would be hugely appreciated.
BACKGROUND:
For a standard Snell's law calculation we can write [itex] n_{1}sinθ_{i} = n_{2}sinθ_{t} [/itex]. All angles are defined relative to the normal.
But when the incident angle [itex]θ_{i}[/itex] exceeds the critical angle [itex]θ_{crit}[/itex], we get total internal reflection (TIR) and the transmitted angle [itex]θ_{t}[/itex] is complex (but still calculable!) and so in general no energy is propagated through the interface. For my application, the evanescent wave which is generated at a TIR interface is important and so I often need to be able to calculate complex [itex]θ_{t}[/itex].
MY PROBLEM:
In the usual case where [itex]θ_{i}[/itex] < [itex]θ_{crit}[/itex], we can obviously define the complement of the transmitted angle [itex]θ_{t}[/itex] as Pi/2 - [itex]θ_{t}[/itex]. This is simply the angle of the refracted ray relative to the interface rather than relative to the normal.
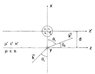
But when [itex]θ_{i}[/itex] > [itex]θ_{crit}[/itex] and [itex]θ_{t}[/itex] is explicitly complex, how can I calculate the "complement" of this? I definitely need a numerical value for this "complement" for subsequent calculations, but I'm not sure how to go about calculating it and I'm driving myself slowly insane because it seems like it should be very simple. The attached sketch might clarify my question.
POSSIBLE SOLUTIONS:
1) Simply taking Pi/2 - [itex]θ_{t}[/itex]. Since this completely ignores the complex component, I simply don't know if this is conceptually sensible but it is what I have been doing.
2) Let [itex]z_{1} = θ_{t}[/itex]. Take the principal argument of [itex]z_{1}[/itex], [itex]Arg|z_{1}|[/itex], to get the [itex]θ[/itex] defined in [itex] z_{1} = r(cos θ + i sin θ)[/itex] since [itex]θ = Arg|z_{1}|[/itex] and then calculate [itex]r[/itex] by rearranging. Note that [itex]r[/itex] shouldn't change under rotation. Calculate [itex]θ_{new} = Pi/2 - θ[/itex] and then substitute this back into [itex] z_{2} = r(cos θ_{new} + i sin θ_{new})[/itex]... so then the angle I want (the "complement") is assumed to be [itex]z_{2}[/itex]... I really don't think this approach makes sense, but it's where my mind has wandered to.
I'm tying myself in knots trying to calculate something I think should be very simple. I'm writing/debugging some code at the moment, and I simply don't know if this silly problem is the source of the major errors I'm currently seeing. Some help would be hugely appreciated.
BACKGROUND:
For a standard Snell's law calculation we can write [itex] n_{1}sinθ_{i} = n_{2}sinθ_{t} [/itex]. All angles are defined relative to the normal.
But when the incident angle [itex]θ_{i}[/itex] exceeds the critical angle [itex]θ_{crit}[/itex], we get total internal reflection (TIR) and the transmitted angle [itex]θ_{t}[/itex] is complex (but still calculable!) and so in general no energy is propagated through the interface. For my application, the evanescent wave which is generated at a TIR interface is important and so I often need to be able to calculate complex [itex]θ_{t}[/itex].
MY PROBLEM:
In the usual case where [itex]θ_{i}[/itex] < [itex]θ_{crit}[/itex], we can obviously define the complement of the transmitted angle [itex]θ_{t}[/itex] as Pi/2 - [itex]θ_{t}[/itex]. This is simply the angle of the refracted ray relative to the interface rather than relative to the normal.
But when [itex]θ_{i}[/itex] > [itex]θ_{crit}[/itex] and [itex]θ_{t}[/itex] is explicitly complex, how can I calculate the "complement" of this? I definitely need a numerical value for this "complement" for subsequent calculations, but I'm not sure how to go about calculating it and I'm driving myself slowly insane because it seems like it should be very simple. The attached sketch might clarify my question.
POSSIBLE SOLUTIONS:
1) Simply taking Pi/2 - [itex]θ_{t}[/itex]. Since this completely ignores the complex component, I simply don't know if this is conceptually sensible but it is what I have been doing.
2) Let [itex]z_{1} = θ_{t}[/itex]. Take the principal argument of [itex]z_{1}[/itex], [itex]Arg|z_{1}|[/itex], to get the [itex]θ[/itex] defined in [itex] z_{1} = r(cos θ + i sin θ)[/itex] since [itex]θ = Arg|z_{1}|[/itex] and then calculate [itex]r[/itex] by rearranging. Note that [itex]r[/itex] shouldn't change under rotation. Calculate [itex]θ_{new} = Pi/2 - θ[/itex] and then substitute this back into [itex] z_{2} = r(cos θ_{new} + i sin θ_{new})[/itex]... so then the angle I want (the "complement") is assumed to be [itex]z_{2}[/itex]... I really don't think this approach makes sense, but it's where my mind has wandered to.