- #1
wutang42
- 3
- 0
Homework Statement
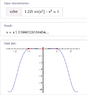
Solve
sin(t2) - t2 =0. for t
Homework Equations
None, besides various trig identities. This was actually a dynamics problem where I had to solve for time, and this is simply the equation you get after summing up all the forces.
The Attempt at a Solution
Now obviously 0 is a solution, and when I plug it into wolfram alpha I get t=1.04, which I know is the correct answer because my professor told us that in class. However, when I plug it into my TI-89, the only solution that comes out is 0, and when I graph it, it doesn't show the 1.04 solution either.So, my question is, is there any way to solve this problem without a numerical solver? And if not, is there any way to plug it into my TI 89 in order to get the correct answer?