Solids of revolution question !

lionely

1. The problem statement, all variables and given/known data
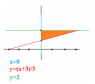
Find the volumes of the solids generated

a) x-3y+3= 0, x=0 , y=2 about the x axis

I sketched the graph got a straight line,

I then proceeded to integrate y²

∏∫y²δx

=[(x^3/27)+(x^2/3)+ (x)] from x=3 to x=-3
I got 8∏
but the answer is 5∏

b) x-y²-1=0, x=2 about the y-axis

∏∫x²δy

= [ (y^5/5) + (2y³/3) + (y)] from x=1 to x=-1

I got (56/15)∏ for this one but the answer is (64/15)∏

iRaid

a) First off, don't memorize these formulas, you have to understand what's going on.
You're asked to find the area between:
y=(x+3)/3, x=0, y=2 about the x-axis
So the graph looks like this:


Now, the way to do this problem is that you need to subtract the outer radius from the inner right?

So what does the integral become?

Attached Thumbnails

 

lionely

Uh is it the intergral of (x/3) +1 - (integral of y=2)?

HallsofIvy

First, it is clear from the graph that the line y= 2 is above the line y= x/3+ 1. Your calculation will give a negative volume!

Second, you want to subtract the volumes, not just the integrals! The volume given by y(x) rotated around the x-axis is [itex]\pi\int y^2 dx[/itex].

iRaid

Adding onto what HallsofIvy said, what you're doing is subtracting the volumes of the two rotations, so technically you can have 2 integrals but they would be:
[tex]\pi\int (outer)^{2}dx-\pi\int (inner)^{2}dx[/tex]
This is just using pi r^2 to find the area of a piece of the circle, the dx would be the width of the circle and the integral because it is the sum of many pieces between 2 points.
Do you see why that works?

lionely

∏∫(4)^2dx− ∏∫(((x/3)+1)^2dx ?

Oh when I do this from x=0 to x=3 I do get 5∏

lionely

I got the 2nd one too. Thanks everyone

iRaid

That's correct.

lionely

Oh may I ask one more question? I think I got the answer but not sure if my method was correct.

Mark44

Which problem are you asking about? If it's the first problem, you can do this in a couple of ways: by "washers" (disks with holes in them) or by cylindrical shells (sort of like the layers in an onion).

Either way should produce the correct answer, but often one way will be easier than the other, so it pays to be comfortable using both ways. Also, the advice given by iRaid to not memorize the integration formulas is good advice. However, you do need to know the formulas for the area of a circle and for the area of a rectangle, both of which are pretty simple.

To get the volume of a disk, it's just the area of the circle times the thickness of the disk, which will usually be either Δx or Δy.
To get the volume of a washer, find the volume of the outer disk, and subtract the volume of the inner disk (the hole).
To get the volume of a shell, you need the area of a rectangle times its thickness. One of the dimensions of the rectangle comes from the circumference of the cylindrical shell, which would be ##2\pi## times the radius of the shell. The length is just the length of the shell, and the thickness is either Δx or Δy.

It is extremely important to draw a picture of the region that will be rotated, and as good a sketch of the solid of revolution as you can manage. If you don't draw these pictures, there's a very good chance that the integral you set up will not produce the correct answer.

lionely

Well the question was to find the volume generated by

y=1/x , y=1 , x=2 about y=0

I did this

∏∫(1/x^2).dx from x=0 to x=2 I got -1/2∏

then ∏∫1.dx =[x] from x=0 to x=2 and I got ∏

then I did this ∏-(1/2)∏ = 1/2∏

is this correct?

Mark44

Do you mean between x = 1 and x = 2?

Also, is the region between the graph of y = 1/x and the x-axis?

Try to be more precise in what you ask.

lionely

Find the volumes of the solids generated when each of the areas enclosed by the following curves and lines is rotated about y=0

y=1/x , y=1 , x=2

Mark44

One of you limits of integration is wrong. Did you sketch the region that is being rotated?

lionely

Uhh I tried I sketched y=1/x and drew in the line y=1

and the region is somewhere between y=1/x and y=1 right?

Mark44

Right, and the region is also bounded by the line x = 2. So where does the curve intersect the line y = 1?

lionely

The curve meets y=1 at x=1